Chunling Jin , Jingjing Liu , Li Gong and Yang Su
Risk Assessment of Diversion Tunnel Construction Based on GRA-EWM-MEE Model
Abstract: In order to accurately predict the level of landslide and water surge risks during the construction phase of the diversion tunnel, a scientific and reasonable assessment of the tunnel construction safety risks was carried out by combining game theory and the matter-element expansion method. Considering the various predisposing indexes of the tunnel, an index system containing 24 indexes was constructed by combining relevant codes and references. GRA and EWM are used to assign subjective and objective weights to the indexes respectively, and game theory is used to determine the weights comprehensively. The GRA-EWM-MEE model was established based on the matter-element extension method and validated with tunnel 7# as an example. The results show that the correlation degrees of each section of the tunnel are: 0.086, 0.069, 0.033, 0.035, and 0.077, all of them belong to class II (moderate risk), which is consistent with the results of the variable fuzzy set evaluation and engineering risk assessment report. Therefore, it is feasible to apply the model to tunnel construction risk assessment, which can provide new ideas for the safety risk assessment of similar diversion tunnels.
Keywords: Diversion Tunnel , Entropy Weight Method , Grey Relational Analysis , Matter-Element Extension Model , Risk Assessment
1. Introduction
A major problem during tunnel construction is how to prevent accidents such as collapse and sudden surges of water, and it is necessary to conduct a comprehensive and reasonable risk assessment of tunnel safety before construction.
Qi et al. [1] established an evaluation index system for hydraulic tunnels in the Northwest region, and used the ideal point grey correlation optimization method for safety evaluation of hydraulic tunnel defects in a long-distance water diversion project safety study. De Silva et al. [2] focused on evaluating the seismic sensitivity curve of circular tunnels under medium to heavy conditions, implementing the finite difference method to provide an effective tunnel during construction. Gong et al. [3] used principal component analysis for probabilistic neural networks to improve the pattern recognition efficiency of neural networks for tunnel safety prediction and assessment. Kunhoth et al. [4] established various evaluation criteria for indoor navigation systems and their future directions. Ferraris et al. [5] propose a model-driven approach based on extending UML and SysML that helps to model smart IoT entities. Singh et al. [6] propose a deep learning-based blockchain-driven secure smart city solution to improve communication broadband for smart factories and smart manufacturing applications in smart cities. Li [7] analyzed the overall structural stability of the tunnel under different construction conditions and different work methods, taking into account indexes such as duration, economy, and quality, and provided a reference for tunnel construction. Lee [8] proposed the use of reinforcement learning algorithms and neural networks to evaluate learning games. However, due to the stochastic and variable nature of tunnel construction, it is difficult to guarantee the accuracy of the results with commonly used methods such as hierarchical analysis, fuzzy integrated evaluation, and back propagation neural networks, so it is important to develop a set of tunnel construction safety risk evaluation models.
In this paper, we propose an evaluation model based on GRA-EWM-MEE for the accurate evaluation of tunnel construction risk levels:
· Constructing the index system, combining relevant norms and references, constructing an evaluation index system containing 24 indexes.
· Combined assignment, using the gray correlation analysis method and the entropy weight method to evaluate the indicators for subjective and objective weight distribution, through game theory optimization to get a comprehensive weight, to avoid the limitations of a single assignment method.
· Risk assessment, according to the established model for the diversion of the Yin Da Ji Huang 7# tunnel construction risk level assessment, the results are consistent with the actual, to prove the feasibility of the model, in order to provide a theoretical basis for the construction safety risk assessment of similar projects.
This paper involves a large number of engineering evaluation methods in the form of abbreviated proper names. To facilitate the reading and understanding of the research content of this paper, the full names of the proper names are given in Table 1.
Table 1.
| Abbreviation | Full name |
|---|---|
| GRA | Grey relational analysis |
| EWM | Entropy weight method |
| MEE | Matter element extension |
This paper is organized as follows: Section 2 establishes the tunnel construction safety evaluation index system. In Section 3, we propose the theoretical approach of the GRA-EWM-MEE model. In Section 4, we use Tunnel 7# as an example to validate the model by example and compare the evaluation results with the variable fuzzy set calculation results and the engineering risk assessment report. Section 5 presents the conclusions of this paper.
2. Tunnel Construction Risk Assessment Index System and Classification
To minimize the damage caused by landslides, sudden surges, and other accidents during the construction of the tunnel, according to the current research results of tunnel construction risk management, consider the pregnant risk environment in tunnel construction, and refer to the “Waterworks Underground Excavation Project Construction Specifications,” “Temporary Regulations on Risk Assessment and Management of Railway Tunnels,” and related literature [9,10], from the external risk and internal risk aspects of the establishment of 24 indexes of the evaluation index system of which the external and internal risk indexes are 12 each. Referring to the classification of production safety accidents in the Regulations on Production Safety Accident Reporting and Investigation and Handling, the construction safety risk level is divided into four levels: low risk (I), moderate risk (II), high risk (III), and extremely high risk (IV), and the index system and classification are shown in Table 2.
Table 2.
| Index | Risk level | |||
|---|---|---|---|---|
| I (low) | II (moderate) | III (high) | IV (extremely high) | |
| External risk | ||||
| Geological conditions | ||||
| Surrounding rock grade [TeX:] $$C_1$$ | (0,1.5] | (1.5,2.5] | (2.5,3.5] | (3.5,4.5] |
| Seismic intensity [TeX:] $$C_2$$ | [1,4) | [4,7) | [7,10) | [10,12] |
| Permafrost depth (cm) [TeX:] $$C_3$$ | [0,40) | [40,80) | [80,120) | [120,200) |
| Hydrological conditions | ||||
| Surface water resources (100 million [TeX:] $$m^3$$) [TeX:] $$C_4$$ | [0,10) | [10,20) | [20,30) | [30,40] |
| Groundwater resource volume ([TeX:] $$m^3$$) [TeX:] $$C_5$$ | [0,5) | [5,15) | [15,30) | [30,40] |
| Climatic conditions | ||||
| Minimum temperature ([TeX:] $${ }^{\circ} \mathrm{C}$$) [TeX:] $$C_6$$ | [0,5) | (-15,0] | (-35,-15] | (-50,-35] |
| Minimum pressure (kPa) [TeX:] $$C_7$$ | (76,100) | (70,76] | (70,65] | (5,65] |
| Altitude (m) [TeX:] $$C_8$$ | (0,1500] | (1500,3500] | (3500,5500] | (5500,7000] |
| Average annual rainfall (mm) [TeX:] $$C_9$$ | (0,200] | (200,600] | (600,1000] | (1000,1500] |
| Environmental conditions | ||||
| Ventilation efficiency [TeX:] $$C_10$$ | (8,10] | (6,8] | (3,6] | (0,3] |
| Drainage efficiency [TeX:] $$C_11$$ | (8,10] | (6,8] | (3,6] | (0,3] |
| Power guarantee rate [TeX:] $$C_12$$ | (8,10] | (6,8] | (3,6] | (0,3] |
| Internal risk | ||||
| Participants | ||||
| Professional level [TeX:] $$C_13$$ | (8,10] | (6,8] | (3,6] | (0,3] |
| Human health effects [TeX:] $$C_14$$ | (8,10] | (6,8] | (3,6] | (0,3] |
| Material equipment | ||||
| Equipment operating rate [TeX:] $$C_15$$ | (8,10] | (6,8] | (3,6] | (0,3] |
| Material operating rate [TeX:] $$C_16$$ | (8,10] | (6,8] | (3,6] | (0,3] |
| Construction process | ||||
| Construction method applicability [TeX:] $$C_17$$ | (8,10] | (6,8] | (3,6] | (0,3] |
| The reasonableness of the form of support [TeX:] $$C_18$$ | (8,10] | (6,8] | (3,6] | (0,3] |
| Technical safety | ||||
| Monitor measurement strength [TeX:] $$C_19$$ | (8,10] | (6,8] | (3,6] | (0,3] |
| Contingency Plan [TeX:] $$C_20$$ | (8,10] | (6,8] | (3,6] | (0,3] |
| Manage security | ||||
| Emergency rescue level [TeX:] $$C_21$$ | (8,10] | (6,8] | (3,6] | (0,3] |
| Risk management level [TeX:] $$C_22$$ | (8,10] | (6,8] | (3,6] | (0,3] |
| Design | ||||
| Hydraulic tunnel span (m) [TeX:] $$C_23$$ | (0,9] | (9,14] | (14,18] | (18,22] |
| Hydraulic tunnel length (km) [TeX:] $$C_24$$ | (0,0.5] | (0.5,3] | (3,10] | (10,15] |
In establishing the indicator system, this paper considers multiple perspectives, systematically and completely identifies the influencing indexes that reflect the basic situation of the project, and considers whether the actual data of each influencing factor is easily available. The established indicator system covers both internal risk indexes, which are caused by human behavioral indexes, and external risk indexes, which are mainly physical influencing indexes. Taking into account the interaction between risk indexes and avoiding duplicate identification, a complete and objective index system is finally obtained.
3. GRA-EWM-MEE Model
Risk evaluation is based on risk identification, a comprehensive analysis of the overall risk, and the construction of risk models. Scholars at home and abroad have used a variety of evaluation methods in the field of risk evaluation, and it is vital to choose the appropriate evaluation method for different problems. Table 3 shows a comparison of the scope of application of several evaluation methods currently in common use.
The tunnel construction safety risk evaluation problem studied in this paper requires an evaluation method with high accuracy and comprehensive identification of risk indexes; therefore, this paper adopts the material element topological model evaluation method.
Table 3.
| Evaluation methods | Features | Scope of application |
|---|---|---|
| BP neural network | Artificial intelligence algorithm | Large sample of data |
| Risk matrix method | Two-dimensional table, quick to use | Requirements for individual risk levels |
| Analytic hierarchy process | Highly subjective | Simple items |
| Fuzzy comprehensive evaluation | Guided by fuzzy mathematics | Fewer risk indexes |
| Decision tree | Intuitive representation of risk types | Fewer risk indexes |
| Matter-element extension | Systematic, risks should not be missed | High accuracy |
3.1 Determine the weight of the index
3.1.1 The GRA method determines the subjective weight
GRA is a multi-factor data statistical analysis method obtained by optimizing based on the grey theory proposed by Lu et al. [11]. It determines the correlation degree of a series based on the similarity of change trends between the corresponding indicators of the series, and its specific steps are as follows:
(1) Determining the analytical series
Reference series: data series reflecting the standard values of each indicator.
Comparative series: A data series consisting of actual data for each sample indicator.
(2) Variable normalization: To avoid the inconvenience of calculations with different scales, the indicator data needs to be normalized.
(3)
[TeX:] $$\left.X_i=\frac{X_{i(k)}}{\bar{X}_\iota} \right\rvert\, k=1,2, . ., n ; i=1,2, \ldots, m$$where k denotes the number of indicators and i denotes the number of samples.
(3) Calculating the number of contacts
(4)
[TeX:] $$\xi_{ik}=\frac{\min _i \min _k\left|y(k)-x_i(k)\right|+\rho \max _i \max _k\left|y(k)-x_i(k)\right|}{\left|y(k)-x_i(k)\right|+\rho \max _i \max _k\left|y(k)-x_i(k)\right|}$$The coefficient of discrimination is the magnitude of the correlation between two data series at a specific moment in time. In general, the smaller the value, the better the resolution, with a value between 0 and 1 being more appropriate, usually 0.5.
(4) Calculating weights
(5)
[TeX:] $$W_1=\frac{\xi_{i k}}{\frac{1}{n} \sum_{k=1}^n \xi_i(k)}, k=1,2, . ., n ; i=1,2, \ldots, m$$3.1.2 The EWM determines the objective weight
The EWM is an objective empowerment method that determines the weight [TeX:] $$W_2$$ of each index by calculating the information entropy of the index [12]. The calculation steps are as follows:
(1) Build a judgment matrix X with n evaluation objects and evaluation metrics:
(6)
[TeX:] $$X=\left[\begin{array}{ccc} x_{11} & \cdots & x_{1 m} \\ \vdots & \ddots & \vdots \\ x_{n 1} & \cdots & x_{n m} \end{array}\right]$$(2) Standardized treatment:
(7)
[TeX:] $$Z_{i j}=\frac{x_{1 j}-\min \left\{x_{1 j}, x_{2 j}, L, x_{n j}\right\}}{\max \left\{x_{1 j}, x_{2 j}, L, x_{n j}\right\}-\min \left\{x_{1 j}, x_{2 j}, L, x_{n j}\right\}}$$(3) Determine the entropy value of the index information [TeX:] $$e_j$$
(8)
[TeX:] $$e_j=-\frac{1}{\ln n} \sum_{i=1}^n p_{i j} \ln \left(\ln p_{i j}\right), j=1,2, . ., m$$Medium: [TeX:] $$p_{i j}=\widetilde{z_{l \jmath}} / \sum_{i=1}^n \widetilde{z_{l \jmath}} .$$
(4) Determine the entropy right of the evaluation index:
3.1.3 Game theory portfolio empowerment
The combination of game theory and empowerment can not only improve the rationality and accuracy of the weight distribution results but also the advantages of the objective empowerment method [13,14]. The calculation steps are as follows:
(1) Calculate the synthetic weight vector [TeX:] $$w_z$$:
where P is the type of weight method, [TeX:] $$\alpha_k$$ is the combined coefficient, [TeX:] $$W_k$$ is [TeX:] $$\left(W_{k i}\right)(k=1,2, \ldots, P, i=1,2, \ldots, n)$$
(2) The countermeasure model optimized for [TeX:] $$\alpha_k$$ is shown in Formula (11), and the conditions for its transformation into the optimal first derivative are as shown in Formula (12):
(12)
[TeX:] $$\left[\begin{array}{cccc} w_1 \cdot w_1^T & w_1 \cdot w_2^T & \ldots & w_1 \cdot w_p^T \\ w_2 \cdot w_1^T & w_2 \cdot w_2^T & \ldots & w_2 \cdot w_p^T \\ \vdots & \vdots & & \vdots \\ w_p \cdot w_1^T & w_p \cdot w_2^T & \ldots & w_p \cdot w_p^T \end{array}\right]\left[\begin{array}{c} \alpha_1 \\ \alpha_2 \\ \vdots \\ \alpha_p \end{array}\right]=\left[\begin{array}{c} w_1 \cdot w_1^T \\ w_2 \cdot w_2^T \\ \vdots \\ w_p \cdot w_p^T \end{array}\right]$$(3) The combined (12) is calculated [TeX:] $$\left(\alpha_k\right)(k=1,2, \ldots, P)$$ and then normalized:
(4) Calculate the evaluation metric [TeX:] $$x_i$$ comprehensive weight:
3.2 MEE Model
The matter-element extension model can be used to solve the problem of the incompatibility of things [15,16].The physical model and the topological set are used to transform the actual problem in the study of the system into a formal problem model and a model describing the process of problem-solving, to effectively solve the contradiction, provide data for decision making, transform the incompatible problem into a compatible problem, and make the problem reasonably solvable. The theory uses an ordered set of three basic quantities R = (N, C, V) to represent the characteristics of a thing, where N represents the name of the thing, C represents the characteristics of the thing, and V represents the value of the quantity of the thing about the characteristics.
3.2.1 Calculate classic domains, sections, and evaluation objects
Classic domain R:
(15)
[TeX:] $$R_j=\left(N_j, C, V_j\right)=\left[\begin{array}{ccc} & C_1 & V_{j 1} \\ & C_2 & V_{j 2} \\ N_j & \vdots & \vdots \\ & C_n & V_{j n} \end{array}\right]=\left[\begin{array}{ccc} & C_1 & {\left[a_{j 1}, b_{j 1}\right]} \\ & C_2 & {\left[a_{j 2}, b_{j 2}\right]} \\ N_j & \vdots & \vdots \\ & C_n & {\left[a_{j 1}, b_{j 1}\right.} \end{array}\right]$$where [TeX:] $$N_j$$ represents the risk level, [TeX:] $$C_i$$ represents the evaluation metric, and [TeX:] $$V_ij$$ represents the j-th level of the index.
Section domain [TeX:] $$R_p:$$
(16)
[TeX:] $$R_p=\left(N_p, C, V_p\right)=\left[\begin{array}{ccc} & C_1 & V_{p 1} \\ & C_2 & V_{p 2} \\ N_p & \vdots & \vdots \\ & C_n & V_{p n} \end{array}\right]=\left[\begin{array}{ccc} & C_1 & {\left[a_{p 1}, b_{p 1}\right]} \\ & C_2 & {\left[a_{p 2}, b_{p 2}\right]} \\ N_p & \vdots & \vdots \\ & C_n & {\left[a_{p 1}, b_{p 1}\right]} \end{array}\right]$$where [TeX:] $$a_{p i}, b_{p i}$$ represents the up operand lower values of the total range of values for the evaluation indexes under each level.
Evaluation meta R:
(17)
[TeX:] $$R=\left[\begin{array}{ccc} & C_1 & V_1 \\ & C_2 & V_2 \\ N_u & \vdots & \vdots \\ & C_n & V_n \end{array}\right]$$3.2.2 Calculate the association function
A correlation function is a function that gives the statistical correlation of a random variable and can express quantitatively and objectively the degree to which something has a certain property and the process of quantitative and qualitative change.
Correlation K:
(18)
[TeX:] $$k_j\left(v_i\right)=\left\{\begin{array}{c} \frac{-\rho\left(v_i, V_{j i}\right)}{\left|V_{i j}\right|}, v_i \in V_{j i} \\ \frac{\rho\left(v_i, V_{j i}\right)}{\rho\left(v_i, V_{p i}\right)-\rho\left(v_i, V_{j i}\right)}, v_i \notin V_{j i} \text {且} \rho\left(v_i, V_{j i}\right) \neq 0 \\ -\rho\left(v_i, V_{j i}\right)-1, v_i \notin V_{j i} \text {且} \rho=0 \end{array}\right.$$
(20)
[TeX:] $$\left\{\begin{array}{c} \rho\left(v_i, V_{j i}\right)=\left|v_i-\frac{\left(a_{j i}+b_{j i}\right)}{2}\right|-\frac{b_{j i}-a_{j i}}{2} \\ \rho\left(v_i, V_{p i}\right)=\left|v_i-\frac{\left(a_{p i}+b_{p i}\right)}{2}\right|-\frac{b_{p i}-a_{p i}}{2} \end{array}\right.$$where [TeX:] $$k_j\left(v_i\right)$$ indicates the degree of correlation between the indexes, [TeX:] $$v_i, V_{j i}, v_i, V_{p i}$$ represents [TeX:] $$v_i$$ and divide interval [TeX:] $$V_{j i},$$ respectively, the distance of the [TeX:] $$V_{p i}$$.
3.2.3 Rating judgment
Determine the risk level by calculating the degree of comprehensive correlation:
where [TeX:] $$K_j(q)$$ represents the degree of comprehensive correlation, and [TeX:] $$W_i$$ represents the comprehensive weight of the index.
3.3 GRA-EWM Meta-Expansion Model Process
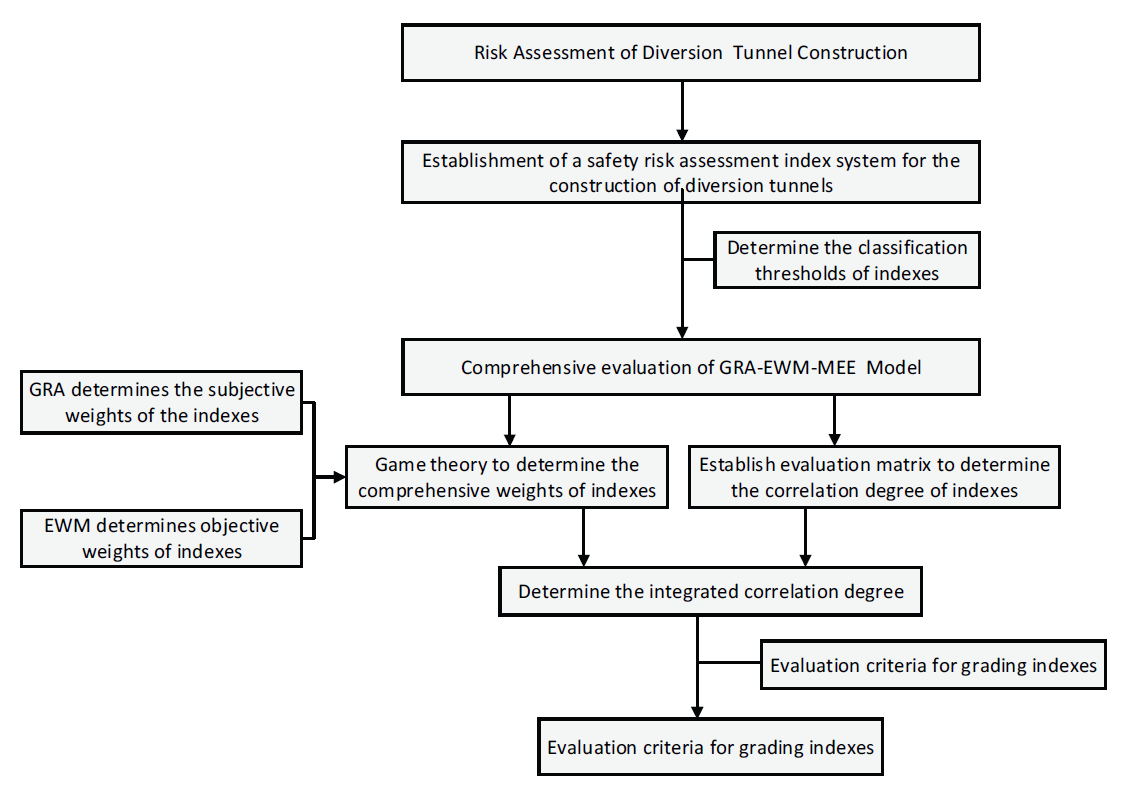
As mentioned above, a comprehensive evaluation model based on GRA-EWM material elements can be developed and applied to the evaluation of the construction safety risk of the 7# tunnel in the third branch of the Yin Da Ji Huang North Trunk Canal Phase II Project. The specific implementation process is as follows:
1) Constructing a comprehensive evaluation index system for tunnel construction risk level based on the analysis of indexes affecting tunnel construction.
2) Calculating the subjective and objective weights of the indexes based on GRA and EWM respectively, and game theory to determine the comprehensive weights of the indexes.
3) Collecting data against the established comprehensive index system to form the original index evaluation matrix, and calculating the correlation degree under each index layer.
4) Determine the final risk level by calculating the comprehensive correlation degree.
The specific implementation process is shown in Fig. 1.
4. Instance Analysis
4.1 Engineering Overview
In this paper, the second phase project of the north trunk canal of the Yin Da Ji Huang 7# tunnel is used as a research object. The tunnel length is 5,632.44 m, section type for the city gate-hole type. The project geological conditions are complex, and prone to flood disasters, in the construction process, the tunnel surrounding rock stability is poor, in the excavation support distance, it must be repeatedly lined, coupled with the fact that the tunnel section is small, residue smoke and other work is difficult, resulting in safety problems occurring frequently in the tunnel construction process. With reference to the construction organization design, geological data and the special tunnel construction program, the tunnel was divided into five typical sections: an inclined shaft section, an inlet section, an upstream section, a downstream section, and an exit section, and the tunnel construction safety risk was assessed for each section. The initial data for this index is shown in Table 4.
Table 4.
| Index | 7# Tunnel section index quantification value | ||||
|---|---|---|---|---|---|
| Slope well | Import | Upstream | Downstream | Exit | |
| [TeX:] $$C_1$$ | 1 | 1 | 4 | 3 | 1 |
| [TeX:] $$C_2$$ | 7 | 7 | 8 | 8 | 7 |
| [TeX:] $$C_3$$ | 87 | 118 | 108 | 97 | 103 |
| [TeX:] $$C_4$$ | 19.97 | 21.61 | 20.54 | 21.57 | 21.42 |
| [TeX:] $$C_5$$ | 13.01 | 12.56 | 12.53 | 13.16 | 12.08 |
| [TeX:] $$C_6$$ | -21 | -28 | -25 | -22 | -32 |
| [TeX:] $$C_7$$ | 76.75 | 77.4 | 74.89 | 75.44 | 77.5 |
| [TeX:] $$C_8$$ | 2700 | 2652 | 2589 | 2788 | 2890 |
| [TeX:] $$C_9$$ | 487.3 | 497.1 | 464.6 | 491.4 | 493.1 |
| [TeX:] $$C_10$$ | 8 | 9 | 9 | 9 | 8 |
| [TeX:] $$C_11$$ | 7 | 7 | 8 | 6 | 8 |
| [TeX:] $$C_12$$ | 9 | 8 | 8 | 7 | 8 |
| [TeX:] $$C_13$$ | 8 | 8 | 9 | 7 | 8 |
| [TeX:] $$C_14$$ | 4 | 8 | 7 | 8 | 9 |
| [TeX:] $$C_15$$ | 8 | 9 | 7 | 8 | 7 |
| [TeX:] $$C_16$$ | 8 | 6 | 5 | 7 | 8 |
| [TeX:] $$C_17$$ | 7 | 7 | 8 | 9 | 8 |
| [TeX:] $$C_18$$ | 8 | 7 | 6 | 9 | 7 |
| [TeX:] $$C_19$$ | 7 | 7 | 7 | 6 | 7 |
| [TeX:] $$C_20$$ | 8 | 6 | 8 | 8 | 7 |
| [TeX:] $$C_21$$ | 7 | 8 | 8 | 7 | 6 |
| [TeX:] $$C_22$$ | 8 | 7 | 6 | 7 | 6 |
| [TeX:] $$C_23$$ | 5.8 | 4.3 | 4.4 | 4.4 | 4.3 |
| [TeX:] $$C_24$$ | 0.41 | 1.89 | 1.21 | 0.9 | 1.9 |
4.2 Weight Calculation
Combined with the initial data of the index, MATLAB programming is used to calculate GRA weight [TeX:] $$W_1$$, EWM weight [TeX:] $$W_2$$, and the GRA-EWM game theory combination empowerment method is used to determine the comprehensive weight W of each index. The specific results are shown in Table 5.
Table 5.
| Index | [TeX:] $$W_1$$(GRA) | [TeX:] $$W_2$$(EWM) | W |
|---|---|---|---|
| [TeX:] $$C_1$$ | 0.0427 | 0.0421 | 0.0427 |
| [TeX:] $$C_2$$ | 0.0422 | 0.0421 | 0.0422 |
| [TeX:] $$C_3$$ | 0.042 | 0.0415 | 0.0419 |
| [TeX:] $$C_4$$ | 0.0411 | 0.0419 | 0.0411 |
| [TeX:] $$C_5$$ | 0.0416 | 0.0416 | 0.0416 |
| [TeX:] $$C_6$$ | 0.0413 | 0.0417 | 0.0413 |
| [TeX:] $$C_7$$ | 0.0414 | 0.0418 | 0.0414 |
| [TeX:] $$C_8$$ | 0.0425 | 0.0415 | 0.0425 |
| [TeX:] $$C_9$$ | 0.0407 | 0.0417 | 0.0407 |
| [TeX:] $$C_10$$ | 0.0412 | 0.0421 | 0.0413 |
| [TeX:] $$C_11$$ | 0.0416 | 0.0416 | 0.0416 |
| [TeX:] $$C_12$$ | 0.0422 | 0.0414 | 0.0421 |
| [TeX:] $$C_13$$ | 0.0423 | 0.0414 | 0.0422 |
| [TeX:] $$C_14$$ | 0.0409 | 0.0414 | 0.041 |
| [TeX:] $$C_15$$ | 0.0424 | 0.0417 | 0.0423 |
| [TeX:] $$C_16$$ | 0.0414 | 0.0416 | 0.0414 |
| [TeX:] $$C_17$$ | 0.0425 | 0.0417 | 0.0424 |
| [TeX:] $$C_18$$ | 0.0423 | 0.0415 | 0.0422 |
| [TeX:] $$C_19$$ | 0.0405 | 0.0415 | 0.0405 |
| [TeX:] $$C_20$$ | 0.0409 | 0.0416 | 0.041 |
| [TeX:] $$C_21$$ | 0.0414 | 0.0416 | 0.0415 |
| [TeX:] $$C_22$$ | 0.0424 | 0.0417 | 0.0423 |
| [TeX:] $$C_23$$ | 0.041 | 0.0415 | 0.0411 |
| [TeX:] $$C_24$$ | 0.0416 | 0.0418 | 0.0416 |
4.3 The Calculation Process of the Meta-Expansion Model
4.3.1 Calculate the correlation of the index and degree of comprehensive correlation
Based on the formula (15–20), take [TeX:] $$X_{11}$$ as an example to calculate the degree of correlation of indexes under each level. The calculation process is as follows:
The correlation is:
If [TeX:] $$-1 \leq k_j\left(v_i\right)\lt 0,$$ indicating that the index does not meet the criteria, but is eligible for conversion to meet the criteria; [TeX:] $$0 \leq k_j\left(v_i\right)\lt 1,$$ indicating that the index meets the criteria, and the higher the value, the closer the index is to the standard requirements. Based on the above calculations, you can know [TeX:] $$k_l\left(N_{01}\right)=0.333, k_l\left(N_{02}\right)=-0.333, k_l\left(N_{03}\right)=-0.6, k_l\left(N_{04}\right)=-0.714,$$ so determine the sloped well segment [TeX:] $$X_{11}$$. The index risk level is I level, the same can be obtained for slope segment other. The correlation between the index and the index layer of the remaining four segments is due to the limited length of Table 6. Only the calculation values of the correlation degree of each index of the sloped well segment are listed, and the results of the correlation degree of the remaining segment indexes are expressed as their corresponding risk level. A comparison of the assessment results and the variable fuzzy set results is shown in Table 7.
Table 6.
| Degree of association | Slope well section | Grade | |||||||
|---|---|---|---|---|---|---|---|---|---|
| [TeX:] $$N_{01}$$ | [TeX:] $$N_{02}$$ | [TeX:] $$N_{03}$$ | [TeX:] $$N_{04}$$ | ||||||
| [TeX:] $$k_i\left(v_1\right)$$ | 0.333 | -0.333 | -0.600 | -0.714 | I | I | IV | III | I |
| [TeX:] $$k_i\left(v_2\right)$$ | -0.417 | 0.167 | -0.125 | -0.389 | II | II | III | III | II |
| [TeX:] $$k_i\left(v_3\right)$$ | -0.351 | -0.074 | 0.088 | -0.275 | III | III | III | III | III |
| [TeX:] $$k_i\left(v_4\right)$$ | -0.333 | 0.003 | -0.002 | -0.334 | II | III | III | III | III |
| … | … | … | … | … | … | … | … | … | … |
| [TeX:] $$k_i\left(v_{23}\right)$$ | 0.356 | -0.356 | -0.586 | -0.678 | I | I | I | I | I |
| [TeX:] $$k_i\left(v_{24}\right)$$ | 0.180 | -0.180 | -0.863 | -0.959 | I | II | II | II | II |
Table 7.
| Section | Meta-expansion model | Variable fuzzy set | |||||
|---|---|---|---|---|---|---|---|
| Degree of comprehensive correlation | [TeX:] $$\overline{\boldsymbol{H}}$$ | Grade | |||||
| [TeX:] $$N_{01}$$ | [TeX:] $$N_{02}$$ | [TeX:] $$N_{03}$$ | [TeX:] $$N_{04}$$ | Grade | |||
| Slope well | -0.185 | 0.086 | -0.252 | -0.540 | II | 1.879 | II |
| Import | -0.200 | 0.069 | -0.199 | -0.530 | II | 1.996 | II |
| Upstream | -0.239 | 0.033 | -0.174 | -0.480 | II | 2.153 | II |
| Downstream | -0.205 | 0.035 | -0.161 | -0.521 | II | 2.017 | II |
| Exit | -0.210 | 0.077 | -0.207 | -0.526 | II | 2.019 | II |
4.3.2 Analysis of the results
As can be seen from the calculation results in the above table, the GRA-EWM-MEE model established in this paper evaluates the construction risk level of this tunnel as level II (moderate risk), and the risk assessment report of this project considers this tunnel to be of medium risk. Combined with the geological indexes and specific construction conditions of tunnel 7#, the main reasons for the tunnel construction safety risk level of II are: tunnel 7# is located in the middle part of the Qilian Mountains uplift zone, which is an alpine region, and the freeze-thaw phenomenon during construction leads to low stability of the surrounding rock and the occurrence of more adverse geological phenomena such as fracture zones. This example shows that the GRA-EWM topology model is a reliable and reasonable risk assessment model for the construction of diversion tunnels, which can effectively identify and assess risk indexes.
5. Conclusion
This study constructed an index system containing 10 sub-systems and 24 indexes. The construction safety risk level of each section of the 7# tunnel of the Yin Da Ji Huang North Main Canal Phase II Project was calculated and analyzed, and the results showed that.
· This study takes tunnel construction safety as the research object and analyzes the risk level of the tunnel construction stage from two major aspects: internal indexes and external indexes. Combining the safety problems in tunnel construction, this study analyzes the risk indexes affecting construction safety in terms of geology, hydrology, and meteorology, classifies the risk level of hydraulic tunnel construction into four levels: low risk (I), medium risk (II), high risk (III), and very high risk (IV), and constructs a diversion tunnel construction safety risk evaluation index system containing 24 indexes.
· Considering that the risk problem is a multi-indicator and multi-level evaluation problem, this study adopts the GRA and EWM to assign subjective and objective weights to the indexes, combines the game theory combination to get a more reasonable and comprehensive weight of the evaluation indexes. The material element topological model was used to construct a safety risk evaluation model for the construction of the diversion tunnel. Compared with other traditional methods, the accuracy is higher, and the risk indexes are less likely to be missed.
· The safety state of tunnel construction is related to external and internal indicators, and the main comprehensive evaluation tools are fuzzy comprehensive evaluation, material element to posable evaluation, cloud model assessment, and Bayesian networks. The existing comprehensive evaluation methods mainly consider the degree of disease, while tunnel health is closely related to people's daily activities and the external environment. Therefore, a comprehensive analysis of the safety state of tunnels in combination with tunnel disease and the causes of the disease is a future research direction for development.
Biography
Biography
Li Gong
https://orcid.org/0000-0002-4824-5109He received a B.S degree from the North China University of Water Resources and Electric Power in 2000, an M.S. degree from Northwest A&F University in 2007, and a Ph.D. degree from Lanzhou Jiaotong University in 2014. Now he is a professor at the School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou, China.
Biography
References
- 1 Y . Qi, C. Jin, and L. Gong, "Safety evaluation of diversion tunnel disease based on ANP-Grey correlation TOPSIS method," Journal of Water Resources and Water Engineering, vol. 2019, no. 1, pp. 143-149, 2019.custom:[[[-]]]
- 2 F. de Silva, S. Fabozzi, N. Nikitas, E. Bilotta, and R. Fuentes, "Seismic vulnerability of circular tunnels in sand," Géotechnique, vol. 71, no. 11, pp. 1056-1070, 2021. https://doi.org/10.1680/jgeot.19.SiP .024doi:[[[10.1680/jgeot.19.SiP.024]]]
- 3 L. Gong, Y . Qi, J. Wang, and S. He, "Application of PCA-PNN model in safety prediction and evaluation of surrounding rock of railway tunnel," Journal of Railway Science and Engineering, vol. 2020, no. 4, pp. 940946, 2020.custom:[[[-]]]
- 4 J. Kunhoth, A. Karkar, S. Al-Maadeed, and A. Al-Ali, "Indoor positioning and wayfinding systems: a survey," Human-centric Computing and Information Sciences, vol. 10, article no. 18, 2020. https://doi.org/10.1186/s1 3673-020-00222-0doi:[[[10.1186/s13673-020-00222-0]]]
- 5 D. Ferraris, C. Fernandez-Gago, and J. Lopez, "A model-driven approach to ensure trust in the IoT," Humancentric Computing and Information Sciences, vol. 10a, article no. 50, 2020. https://doi.org/10.1186/s13673020-00257-3doi:[[[10.1186/s13673020-00257-3]]]
- 6 S. K. Singh, A. E. Azzaoui, T. W. Kim, Y . Pan, and J. H. Park, "DeepBlockScheme: a deep learning-based blockchain driven scheme for secure smart city," Human-centric Computing and Information Sciences, vol. 11, article no. 12, 2021. https://doi.org/10.22967/HCIS.2021.11.012doi:[[[10.22967/HCIS.2021.11.012]]]
- 7 J. Li, "Study on the overall stability evaluation of tunnels under multi-construction method conditions," Construction Safety, vol. 37, no. 2, pp. 32-35, 2022.custom:[[[-]]]
- 8 D. Lee, "Comparison of reinforcement learning activation functions to improve the performance of the racing game learning agent," Journal of Information Processing Systems, vol. 16, no. 5, pp. 1074-1082, 2020. https://doi.org/10.3745/JIPS.02.0141doi:[[[10.3745/JIPS.02.0141]]]
- 9 Z. Ou, H. Fu, Z. Huang, F. Zhang, and T. Zhao, "Comprehensive risk assessment method for shallow underground tunnel construction," Journal of Railway Science and Engineering, vol. 16, no. 9, pp. 23682377, 2019.custom:[[[-]]]
- 10 Z. Gui, Z. Wu, Q. Yan, and C. Zhang, "Research on optimization of highway tunnel construction safety risk assessment method," Journal of Safety Science and Technology, vol. 14, no. 9, pp. 136-143, 2018.custom:[[[-]]]
- 11 J. Lu, L. Ren, D. Rong, and X. Guo, "Risk assessment of coal mine gas explosion based on grey-matterelement model," China Safety Science Journal, vol. 31, no. 2, pp. 99-105, 2021. https://doi.org/10.16265/j. cnki.issn1003-3033.2021.02.014doi:[[[10.16265/j.cnki.issn1003-3033.2021.02.014]]]
- 12 R. Zhu, L. Sun, S. Zhao, Z. Xie, X. Liu, and X. Yin, "Preliminary studies on nitrous oxide emissions from the ornithogenic soils on Xi-sha atoll, South China Sea," Journal of Environmental Sciences, vol. 17, no. 4, pp. 551-556, 2005. https://doi.org/110.3321/j.issn:1001-0742.2005.04.005doi:[[[110.3321/j.issn:1001-0742.2005.04.005]]]
- 13 G. Su, X. Fu, and T. Liu, "Application of improved game theory comprehensive weight in comprehensive evaluation of dam safety," China Rural Water and Hydropower, vol. 2014, no. 11, pp. 82-85, 2014. https://doi.org/10.3969/j.issn.1007-2284.2014.11.022doi:[[[10.3969/j.issn.1007-2284.2014.11.022]]]
- 14 A. Tahmasebi and H. Pourghassem, "Robust intra-class distance-based approach for multimodal biometric game theory-based rank-level fusion of ear, palmprint and signature," Iranian Journal of Science and Technology, Transactions of Electrical Engineering, vol. 41, pp. 51-64, 2017. https://doi.org/10.1007/s40998017-0017-5doi:[[[10.1007/s40998017-0017-5]]]
- 15 P . Sun and S. Rong, "Study on risk assessment model of water inrush in coastal gold mine based on improved matter element extension method," Nonferrous Metal Engineering, vol. 2021, no. 6, pp. 109-117, 2021. https://doi.org/10.3969/j.issn.2095-1744.2021.06.016doi:[[[10.3969/j.issn.2095-1744.2021.06.016]]]
- 16 T. Wang, D. Xu, X. Zhang, J. Fu, and X. Zhang, "Extension evaluation and early warning of shield tunnel excavation face collapse," Journal of Safety and Environment, vol. 20, no. 6, pp. 2052-2059, 2020. https://doi.org/10.13637/j.issn.1009-6094.2019.1366doi:[[[10.13637/j.issn.1009-6094.2019.1366]]]