Ke Yuan , Keke Duanmu , Jian Ge , Bingcai Zhou and Chunfu Jia
A Controllable Parallel CBC Block Cipher Mode of Operation
Abstract: To address the requirement for high-speed encryption of large amounts of data, this study improves the widely adopted cipher block chaining (CBC) mode and proposes a controllable parallel cipher block chaining (CPCBC) block cipher mode of operation. The mode consists of two phases: extension and parallel encryption. In the extension phase, the degree of parallelism n is determined as needed. In the parallel encryption phase, n cipher blocks generated in the expansion phase are used as the initialization vectors to open n parallel encryption chains for parallel encryption. The security analysis demonstrates that CPCBC mode can enhance the resistance to byte-flipping attacks and padding oracle attacks if parallelism n is kept secret. Security has been improved when compared to the traditional CBC mode. Performance analysis reveals that this scheme has an almost linear acceleration ratio in the case of encrypting a large amount of data. Compared with the conventional CBC mode, the encryption speed is significantly faster.
Keywords: Edge Amplitude , Image Restoration , Kernel , Spatial Scale , Windowed-Total-Variation
1. Introduction
The perception of data on the Internet of Things [1] and the storage and utilization of data by cloud computing [2] have promoted the emergence of the big data era, which provides valuable judgment ability by analyzing data quickly. The analysis technology of massive data has garnered significant attention. Data has been scaling up to the TB level, with high-value data becoming a crucial competitive asset. At the same time, the security and availability of data are also facing new challenges. Developing high-speed mass data encryption technology is crucial for maintaining data confidentiality and preventing unauthorized tampering.
At present, the main scheme of big data encryption is the combination of the block cipher [3] and the public key cryptosystem [4]. Typically, the block cipher is used to encrypt large data first, and then the public key cryptography is used to encrypt and protect the key of the block cipher. In 1980, the National Bureau of Standards (now NIST) introduced four modes of operation for block ciphers [5]. They are electronic codebook (ECB), cipher block chaining (CBC), cipher feedback (CFB), and output feedback (OFB). On this basis, various modes have been proposed, such as offset codebook (OCB) [6], integrity aware parallelizable mode (IAPM) [7], EAX [8], etc.
Among them, CBC mode is simple and easy to operate and has better security than other modes of operation with the security of choosing plaintext attacks. Moreover, the duplicate plaintext block does not reveal this duplication in the ciphertext, thus avoiding certain limitations of ECB mode. Therefore, CBC mode is extensively utilized, and big data encryption is also often used in CBC mode.
CBC mode encrypts one plaintext block at a time, using the same key k for each encryption. The input of the encryption algorithm is the XOR of the current plaintext block and the previous ciphertext block. However, for the first block, the input is XOR of the first plaintext block and a random initialization vector IV.
The plaintext block in CBC mode is marked as [TeX:] $$m_i.$$ The corresponding ciphertext block is denoted as [TeX:] $$c_i(1 \leq i \leq s),$$ and s is the total number of blocks. Then, the encryption equation for CBC mode is as follows:
(1)
[TeX:] $$c_i=\left\{\begin{array}{ll} E_k\left(m_1 \oplus I V\right), &i=1 \\ E_k\left(m_i \oplus c_{i-1}\right), &i \geq 2 \end{array} .\right.$$The decryption equation is
(2)
[TeX:] $$m_i= \begin{cases}I V \oplus D_k\left(c_1\right), &i=1 \\ c_{i-1} \oplus D_k\left(c_i\right), &i \geq 2\end{cases}.$$It can be seen that there is feedback iteration in CBC mode, which falls under serial encryption and limits the speed of data encryption. However, in the era of big data, data has the characteristics of large volumes and diverse types. Conventional encryption technology has some restrictions on the speed of encryption. Therefore, it is crucial to develop a parallel cryptography system that incorporates parallel computing theory [9] to effectively encrypt massive data and ensure the security of core data.
This paper proposes a new mode called controllable parallel cipher block chaining (CPCBC) mode, which allows for flexible control over the degree of parallelism to enhance encryption speed in CBC mode. The linear acceleration ratio can be almost achieved without changing the cryptographic characteristics of the original block cipher mode of operation.
2. Related Work
In 2015, El-Semary and Azim [10] proposed a novel block cipher mode of operation known as the counter chain (CC) mode. It integrates the CBC block cipher mode of operation with the counter (CTR) mode in a consistent way. The mode of operation addresses the limitations of parallelization in the CBC mode and the dependency on chaining in the counter mode.
In 2018, Sahi et al. [11] proposed a mode called parallel block cipher (PBC), which allows for the parallel processing of cipher blocks. The PBC mode demonstrated a 60% reduction in execution time compared to the CBC mode. Furthermore, the hash value of the data file might be utilized to provide an integrity check in addition to encryption using AES-128.
Although both modes of operation improve encryption speed, they fail to fully take advantage of the benefits of parallel multiprocessing. The mode proposed in this paper allows for flexible control of parallelism according to requirements, resulting in an acceleration ratio that is nearly linear.
3. Notations
For ease of expression, some of the notations in this paper are presented in Table 1.
Table 1.
| Notation | Description | Notation | Description |
|---|---|---|---|
| [TeX:] $$m_i$$ | Plaintext block in CBC mode | [TeX:] $$c_i$$ | Ciphertext block in CBC mode |
| [TeX:] $$m_j^i$$ | Plaintext block in CPCBC mode | [TeX:] $$c_j^i$$ | Ciphertext block in CPCBC mode |
| [TeX:] $$m_j^i[x]$$ | xth byte of plaintext [TeX:] $$m_j^i$$ | [TeX:] $$c_j^i[i]$$ | xth byte of ciphertext [TeX:] $$c_j^i$$ |
| IV | Initialization vector | k | Key |
| l | Block length | s | Total number of blocks |
| [TeX:] $$E_k\left(m_j^i\right)$$ | Encrypt plaintext block [TeX:] $$m_j^i$$ with key k | [TeX:] $$D_k\left(c_j^i\right)$$ | Decrypt ciphertext block [TeX:] $$c_j^i$$ with key k |
| [TeX:] $$a \| b$$ | Joining operation of strings a and b | [TeX:] $$|m|$$ | Length of plaintext m |
The superscript i and the subscript j of the plaintext block [TeX:] $$m_j^i$$ and ciphertext block [TeX:] $$c_j^i$$ determine the rows and columns in which the block is located.
4. CPCBC Mode of Operation
The core idea behind the CPCBC mode involves the creation of new encryption chains by utilizing specific ciphertext as initialization vectors. The CPCBC mode comprises of two phases: extension and parallel encryption. Before encryption, the plaintext must be padded with PKCS#7 padding scheme [12].
Based on the subscript [TeX:] $$x\left(1 \leq x \leq s, s=\left\lfloor\frac{|m|}{l}\right\rfloor+1\right)$$ of the xth plaintext block [TeX:] $$m_x$$ in the CBC mode, the superscript i and the subscript j of [TeX:] $$m_j^i \text { and } c_j^i$$ can be determined in the CPCBC mode: [TeX:] $$i=\left\lceil\frac{x}{n}\right\rceil \text {, }$$ [TeX:] $$j=\left\{\begin{array}{ll} x \bmod n, &x \bmod n \neq 0 \\ n, &x \bmod n=0 \end{array} .\right.$$
4.1 Outline of the Mode
The encryption equation for CPCBC mode is:
(3)
[TeX:] $$c_j^i= \begin{cases}E_k\left(m_1^1 \oplus I V\right), &i=1 \text { and } j=1 \\ E_k\left(m_j^1 \oplus c_{j-1}^1\right), &i=1 \text { and } j \geq 2 . \\ E_k\left(m_j^i \oplus c_j^{i-1}\right), &i \geq 2\end{cases}$$The decryption equation is:
(4)
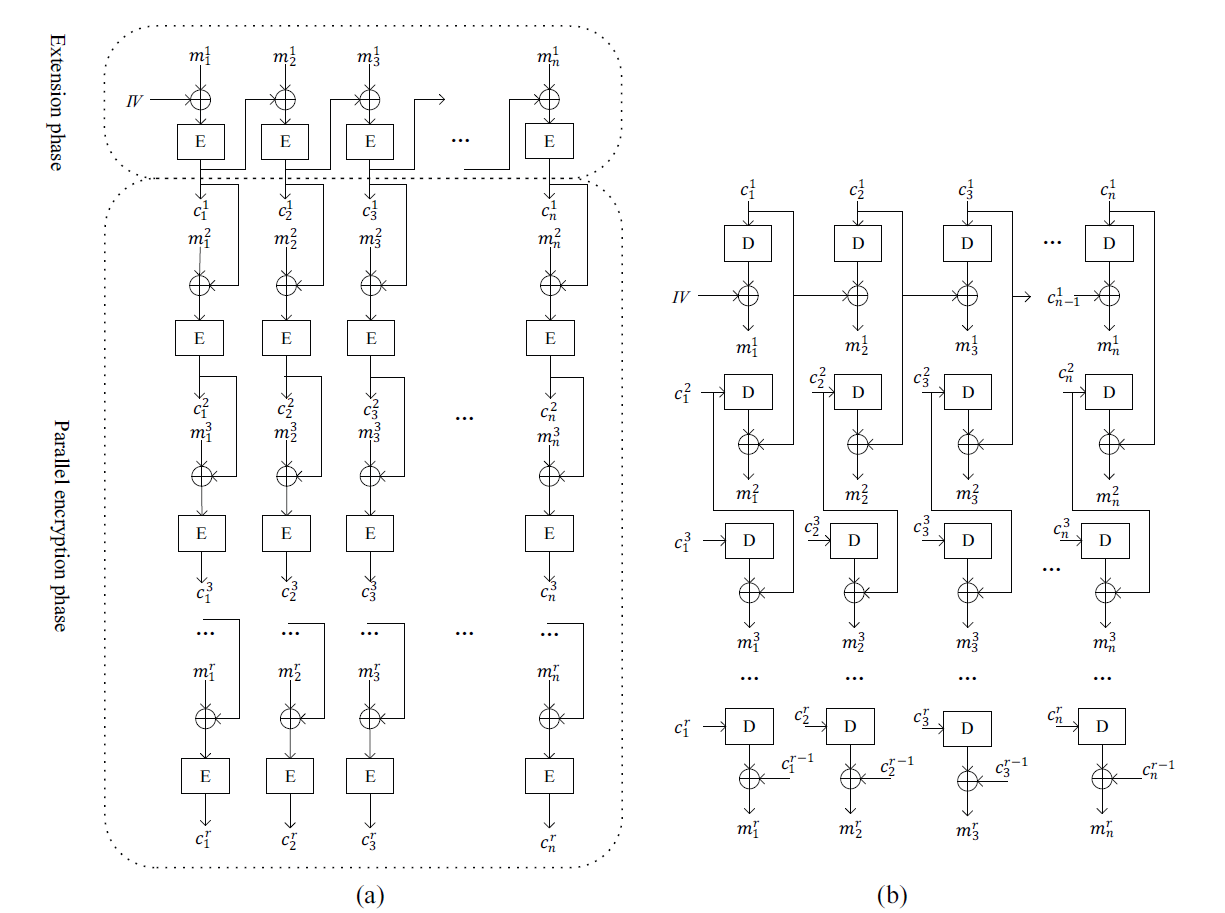
[TeX:] $$m_j^i=\left\{\begin{array}{l} D_k\left(c_1^1\right) \oplus I V, \quad i=1 \text { and } j=1 \\ D_k\left(c_j^1\right) \oplus c_{j-1}^1, \quad i=1 \text { and } j \geq 2 \\ D_k\left(c_j^i\right) \oplus c_j^{i-1}, \quad i \geq 2 \end{array}\right..$$The encryption and decryption diagrams of the CPCBC mode are shown in Fig. 1.
For the last line in encryption mode, the ideal case is when the number of plaintext blocks is evenly divisible by the parallelism n, as shown in Fig. 1(a). In actual encryption, the number of plaintext blocks on the last line is [TeX:] $$d=\left\{\begin{array}{ll} n, &s \bmod n=0 \\ s \bmod n, &s \bmod n \neq 0 \end{array} .\right.$$
The CPCBC mode encryption algorithm is presented in Algorithm 1 and the decryption algorithm is presented in Algorithm 2.
4.2 Extension Phase
In CPCBC mode, i = 1 is called the extension phase, as shown in Fig. 1(a). For the plaintext block [TeX:] $$m_{j-1}^1 \text { and } m_j^1(2 \leq j \leq n)$$ in the extension phase, [TeX:] $$m_{j-1}^1$$ represents the preceding block of [TeX:] $$m_j^1$$, and [TeX:] $$m_j^1$$ is the successor block of [TeX:] $$m_{j-1}^1$$.
The parallelism n is determined based on the number of processors in the actual encryption scenario and the encryption requirements. By ranking n blocks per row, the total number of rows can be determined as [TeX:] $$r=\left\lceil\frac{s}{n}\right\rceil .$$ In this phase, the first n blocks, i.e., [TeX:] $$m_j^1(1 \leq j \leq n),$$ must be encrypted according to the CBC mode, which are the n blocks in the first row. Then, the encryption equation is [TeX:] $$c_j^1=\left\{\begin{array}{l} E_k\left(m_1^1 \oplus I V\right), \quad j=1 \\ E_k\left(m_j^1 \oplus c_{j-1}^1\right), \quad 2 \leq j \leq n \end{array} .\right.$$ The decryption equation is [TeX:] $$m_j^1=\left\{\begin{array}{l} D_k\left(c_1^1\right) \oplus I V, \quad j=1 \\ D_k\left(c_j^1\right) \oplus c_{j-1}^1, \quad 2 \leq j \leq n \end{array} 002 \mathrm{E}\right.$$
4.3 Parallel Encryption Phase
In CPCBC mode, [TeX:] $$i \geq 2$$ is called a parallel encryption phase, as shown in Fig. 1(a). For the plaintext block [TeX:] $$m_j^{i-1} \text { and } m_j^i(1 \leq j \leq n)$$ in the parallel encryption phase, [TeX:] $$m_j^{i-1}$$ represents the preceding block of [TeX:] $$m_j^i, \text { and } m_j^i$$ is the successor block of [TeX:] $$m_j^{i-1}.$$ The preceding and successor blocks in the parallel encryption phase are n blocks apart in the combined ciphertext due to the arrangement of the plaintext and ciphertext in rows.
During this phase, the n ciphertext blocks generated in the extension phase are utilized as initialization vectors to open n parallel encryption chains. These chains exhibit independent and parallel relationships. In the same chain, the encryption remains in CBC mode. Then, the encryption equation for the parallel encryption phase is [TeX:] $$c_j^i=E_k\left(m_j^i \oplus c_j^{i-1}\right), i \geq 2,1 \leq j \leq n .$$ The decryption equation is [TeX:] $$c_j^i=D_k\left(c_j^i\right) \oplus c_j^{i-1}, \quad i \geq 2,1 \leq j \leq n .$$
5. Security Analysis
The phases of this scheme, the extension phase and the parallel encryption phase, are essentially still CBC modes. The extension phase generates ciphertext [TeX:] $$c_1^1, c_2^1, \cdots, c_n^1$$ serially. Then, these n blocks are used as initialization vectors for the parallel encryption phase, allowing for the opening of n parallel encryption chains. Due to the good randomness of ciphertext and the dependence on plaintext m and initialization vector IV, the encryption result becomes highly unpredictable. Therefore, this mode of operation preserves the security features of the conventional CBC mode, which has been proven to be secure under the left-or-right chosen plaintext attack (LOR-CPA) model [13].
Therefore, we will not focus on demonstrating the security of this scheme from the point of provable security, but instead, we will examine it from the point of attack route. Currently, there are more effective attack schemes against CBC mode, such as the byte-flipping attack (BFA) and padding oracle attack (POA). The security of CPCBC mode is analyzed from these two attacks.
5.1 Byte-Flipping Attack
The core idea of the BFA is to use the influence of the preceding ciphertext block on the latter to achieve plaintext tampering at specific locations. According to the decryption equation of CPCBC mode mentioned above, specifically Eq. (4), the encryption of the first plaintext block occurs after XOR with the initialization vector IV, while the encryption of the following plaintext block occurs after XOR with the previous block.
Theorem 1. Under the condition that parallelism n is not public, the BFA can still attack CPCBC mode, and the attack cost is proportional to n.
Proof. Since BFA only considers the relationship between preceding and successor blocks, they are referred to as N-1 and Nth blocks. Based on the value A of one bit of the N-1th ciphertext block and the decrypted value B of the same position of the Nth ciphertext block, the plaintext C of the Nth plaintext block at that position can be easily obtained.
If we XOR A with C, a new A can be obtained and can be marked as [TeX:] $$A^{\prime}=A \oplus C.$$ Replacing [TeX:] $$A \text { with } A^{\prime}$$ in Eq. (5), the following equation can be derived from the property of XOR.
Thus, the calculated plaintext has been tampered with and altered to 0. In addition, the plaintext can be freely changed to any character X. We only need to XOR [TeX:] $$A^{\prime}$$ with X and obtain [TeX:] $$A^{\prime \prime}=A^{\prime} \oplus X=A \oplus C \oplus X.$$ Similarly, the following equation can be obtained according to Eq. (5):
At this point, the plaintext has been changed to any desired character by modifying the ciphertext. For the first block, use this principle to change IV. In particular, during the extension phase of CPCBC mode, [TeX:] $$c_j^1(1 \leq j \leq n-1)$$ is used not only for XOR with [TeX:] $$m_{j+1}^1,$$ but also for XOR with [TeX:] $$m_j^2.$$ This may cause confusion for potential attackers attempting to tamper with the plaintext in both places.
Given certain known plaintext and ciphertext, along with the ability to locate the preceding ciphertext block, BFA enables tampering with the plaintext at a specific location. According to the ciphertext layout in CPCBC mode (shown in Fig. 1(a)), n blocks are separated between [TeX:] $$c_j^i$$ in the parallel encryption phase and its preceding block [TeX:] $$c_j^{i-1}.$$ If parallelism n is not made public, an attacker would have to go through additional operations to enumerate the value of n in order to achieve plaintext tampering. As the value of n increases, cracking the attacker becomes more challenging. The average attack time is proportional to n.
Therefore, compared with the conventional CBC mode, the CPCBC mode proposed in this paper is more resistant to BFA, and the security has some improvement.
5.2 Experiments on Real Images
The POA involves a recipient who decrypts the received ciphertext and verifies if the decrypted result satisfies the padding rule. If it does, the recipient returns "Valid"; otherwise, they return "Invalid." Vaudenay [14] developed this method to attack CBC mode which utilizes the response messages of ciphertext padding verification. Based on this idea, the POA against CPCBC mode is described below.
Theorem 2. Under the condition that parallelism n is not public, POA can still attack CPCBC mode, and the attack cost of Step 1 is proportional to n.
Proof. Suppose that the last plaintext block in CPCBC mode is [TeX:] $$m_d^r\left(1 \leq d \leq n, r=\left\lceil\frac{s}{n}\right\rceil\right) .$$ Its preceding block is denoted as [TeX:] $$m_d^{r-1}.$$ The corresponding ciphertext blocks are [TeX:] $$c_d^r \text { and } c_d^{r-1},$$ respectively. The intermediate result of decrypting the ciphertext block [TeX:] $$c_j^i$$ with symmetric key k is marked as [TeX:] $$m_j^{i^{\prime}},$$ which indicates that [TeX:] $$m_j^{i^{\prime}}=D_k\left(c_j^i\right).$$ The preceding block of [TeX:] $$c_j^i \text { is } c_j^{i-1}.$$ Then, the Eq. (3) becomes [TeX:] $$m_j^i=m_j^{i^{\prime}} \oplus c_j^{i-1}.$$ [TeX:] $$m_j^i=m_j^{i^{\prime}} \oplus c_j^{i-1}.$$
When r = 1 or n = 1, CPCBC mode degenerates to CBC mode, and the attack method is the same as that in [14]. Therefore, the discussion below is based on [TeX:] $$r \geq 2 \text { and } n \geq 2.$$
If the parallelism n is public, [TeX:] $$m_d^{r-1},$$ the preceding block of [TeX:] $$m_d^r,$$ is easily located. The attack process is as follows:
Step 1 (Determine the padding length of the last block): The last block [TeX:] $$c_d^r$$ is certain to contain padding, at least a “0x01” and at most sixteen “0x10” (take AES for example). The padding length is marked as L with an initial value of 16, which is hexadecimal 0x10. An attacker starts with the first byte to the left of its preceding block [TeX:] $$c_d^{r-1}$$ and modifies it to:
Then, the modified ciphertext is sent to the recipient. The receiver performs the decryption process and obtains the first byte on the left as [TeX:] $$m_d^{r *}[0]=m_d^{r{ }^{\prime}}[0] \oplus c_d^{r-1^{\prime}}[0]=m_d^{r^{\prime}}[0] \oplus c_d^{r-1}[0] \oplus L=m_d^r[0] \oplus L .$$
At this point, if the recipient returns “Invalid,” [TeX:] $$m_d^{r *}[0]$$ is part of the padding, and the padding length is L. If the “Valid” is returned, then the change in [TeX:] $$c_d^{r-1}[0]$$ does not affect the padding verification. The padding length is guaranteed to be smaller than L. The attacker then modifies the next byte by imitating Eq. (4), subtracts L by one, and transmits it to the receiver again. The above operations are repeated until the “Invalid” result is returned, which will determine the padding length L.
Step 2 (Crack the plaintext of the last block): Once the padding length is obtained, the attacker can decipher the plaintext one by one from right to left. From PKCS#7, the last L bytes of the last block are all L, [TeX:] $$m_d^r[i]=L(16-L \leq i\lt 16).$$ The attacker first modifies the last L bytes of [TeX:] $$c_d^{r-1}.$$
The value range of i is [TeX:] $$16-L \leq i\lt 16.$$ Then, the receiver performs the decryption process and obtains the last L bytes as [TeX:] $$m_d^r[i]^*=m_d^r[i]^{\prime} \oplus c_d^{r-1^{\prime}}[i]=m_d^r[i]^{\prime} \oplus C_d^{r-1}[i] \oplus m_d^r[i] \oplus(L+1)=m_d^r[i] \oplus m_d^r[i] \oplus(L+1)=L+1.$$
Therefore, the effect of Eq. (9) is equivalent to changing the values of the last L bytes of the last plaintext block to L+1 after decryption. Then, the attacker tries to do the following for the last L+1th byte of [TeX:] $$c_d^{r-1} .$$
The effect of the recipient execution is as follows:
(11)
[TeX:] $$\begin{aligned} m_d^r[15-L]^* &=m_d^r[15-L]^{\prime} \oplus c_d^{r-1^{\prime}}[15-L] \\ &=m_d^r[15-L]^{\prime} \oplus c_d^{r-1}[15-L] \oplus X \\ &=m_d^r[15-L] \oplus X \end{aligned}$$The range of X is 0x00-0xFF. There is only one X in this interval so that [TeX:] $$m_d^r[15-L]^*=L+1,$$ which indicates that the last L+1 bytes are also L+1. At this point, the entire block ends with the byte L+1, the number of which is also L+1. It is the only case where "Invalid" does not occur. According to Eq. (11):
Thus, as long as X is known, the attacker can calculate that the last L+1th byte is [TeX:] $$(L+1) \oplus X.$$ Then, the attacker adds 1 to L and repeats this process to obtain the plaintext of the last block. It can be seen that, on average, 128 modified ciphers are sent in order to crack each plaintext byte under this attack method.
Step 3 (Crack the plaintext that is not the last block): For non-tail blocks, there is no essential difference in the attack method. The attacker removes the last block that just cracked. At this time, [TeX:] $$c_{d-1}^r$$ becomes the tail block and [TeX:] $$c_{d-1}^{r-1}$$ is its precursor block. The attacker changes the last byte of [TeX:] $$c_{d-1}^{r-1}$$ according to Eq. (10), [TeX:] $$c_{d-1}^{r-1^{\prime}}[15]$$, and transmits the modified ciphertext to the receiver. If “Invalid” is received, the attacker tries the next X. If “Valid” is received, the following two situations need to be distinguished:
① If the last byte [TeX:] $$m_{d-1}^r{ }^*[15]$$ is 0x01 after decryption, it is guaranteed that “Valid” will be returned. Because padding must exist, and 0x01 is the only single-byte padding that can pass the verification. From Eq. (12), the following can be obtained:
② If the decrypted last byte [TeX:] $$m_{d-1}^r{ }^*[15]$$ is a value between 0x02 and 0x10, and the plaintext happens to be one of the following 15 cases, the “Valid” will also be returned (Table 2).
Table 2.
| Padded bytes | Styles (xx stands for the placeholder) |
|---|---|
| 0x02 | xx xx xx xx xx xx xx xx xx xx xx xx xx xx 02 xx |
| 0x03 | xx xx xx xx xx xx xx xx xx xx xx xx xx 03 03 xx |
| … | …… |
| 0x0F | xx 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F 0F xx |
| 0x10 | 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 xx |
To distinguish between these two cases, after receiving "Valid," the attacker modifies the penultimate byte [TeX:] $$c_{d-1}^{r-1}[14] \text { of } c_{d-1}^{r-1}$$ and resends it to the receiver. In case ①, the receiver still returns "Valid," because the change of the penultimate byte does not affect the format; however, in case ②, the change of the penultimate byte destroys the format, and the receiver returns "Invalid." From this, two cases can be identified, and then Eq. (12) can be applied.
Next, to crack other plaintext sections that are not the tail block, the attacker can repeat Step 2, refer to Eqs. (9)–(12), and crack byte-by-byte from right to left.
The attack during the parallel encryption phase can be accomplished in Steps 1, 2, and 3. Then, the attacker removes the cracked blocks and the remaining extension phase degenerates into CBC mode. Its attack method is identical to the one described in the study [14].
If the parallelism n is not public, the attacker needs to enumerate the value of n step-by-step to locate the preceding block of [TeX:] $$m_d^r.$$ As the value of n increases, it becomes increasingly challenging for an attacker to crack. In order for the attack to be successful, the attacker must enumerate the value of n while proceeding with Step 1. If the attacker modifies all bytes in the preceding block and only receives "Valid" in an attempt to n, it indicates that the modification of the preceding block had no impact on the tail block and suggests that the value of n is incorrect. The attacker persists in attempting n+1 until a "Invalid" response is received, in order to determine the correct value of n. During this process, the number of times an attacker will modify is proportional to n.
Therefore, compared with CPCBC mode with traditional CBC mode, it is evident that CPCBC mode is more resistant to this attack and provides a certain level of security improvement. In addition, this attack is a result of improper design scenes that can be cracked through side channel attack, rather than being a flaw in the algorithm itself.
6. Performance Analysis
In this section, we first analyze the encryption speed of CPCBC mode through mathematical methods and then validate the analysis through experiments.
6.1 Theoretical Analysis
The encryption speed is a crucial factor in evaluating the performance of a block cipher mode of operation. The performance of CPCBC mode is analyzed by comparing the encryption time of the same plaintext between CBC and CPCB.
Theorem 3. Compared with CBC mode, CPCBC mode has an approximate linear acceleration ratio of n.
Proof. Suppose m represents the plaintext to be encrypted. [TeX:] $$|m|$$ represents the length of m, and l is the block length, which is dependent on the selected encryption algorithm. With the PKCS#7 padding scheme, the total number of blocks is [TeX:] $$s=\left\lfloor\frac{|m|}{l}\right\rfloor+1.$$ Note that the processing time for a single block is t, including the time for XOR and encryption operations. In the CBC mode, when the plaintext is m, the total encryption time is as follows:
The number of plaintext blocks in the extension phase of CPCBC mode is n. According to Eq. (14), the encryption time of the extension phase is [TeX:] $$T_1=t n.$$ The time spent in the parallel encryption phase is determined by the maximum time spent in n encryption chains. The maximum time depends on the maximum number of plaintext blocks in these n chains. The maximum number of plaintext blocks for this stage is [TeX:] $$s_{\max }=\left\lceil\frac{s}{n}\right\rceil-1,$$ excluding the block in the extension phase. Then, the encryption time of the parallel encryption phase is [TeX:] $$T_2=t \cdot s_{\max }=t\left(\left\lceil\frac{s}{n}\right\rceil-1\right).$$ Thus, in the CPCBC mode, when the plaintext is m, the total encryption time is as follows:
Definition 1. The definition of speedup is as follows:
[TeX:] $$T_{C B C}$$ represents the encryption time required by the CBC mode and [TeX:] $$T_{C P C B C}$$ is the encryption time required by the CPCBC mode.
Substitute Eqs. (14) and (15) into the definition, the speedup becomes [TeX:] $$S=\frac{\left\lfloor\frac{|m|}{l}\right\rfloor+1}{n+\left\lceil\frac{s}{n}\right\rceil-1}.$$ In this equation, [TeX:] $$s=\left\lfloor\frac{|m|}{l}\right\rfloor+1.$$ Make an approximate calculation of the equation and the speedup is as follows:
(17)
[TeX:] $$S=\frac{\left\lfloor\frac{|m|}{l}\right\rfloor+1}{n+\left[\frac{S}{n}\right\rfloor-1} \approx n\left(1-\frac{n^2 l+1}{|m|+n^2 l+l-1}\right) .$$For commonly used symmetric encryption algorithms, the value of l will not be excessively large. For instance, the SM4 algorithm has a block length of 128 bits, while the AES algorithm offers block lengths of 128, 192, or 256 bits. For parallelism n, the value of n cannot be excessively large due to the actual processor cost. For encryption of large amounts of data, [TeX:] $$|m|$$ is much larger than l and n. Thus, we can obtain:
(18)
[TeX:] $$\lim _{|m| \rightarrow \infty}\left[n\left(1-\frac{n^2 l+1}{|m|+n^2 l+l-1}\right)\right]=n.$$That is, when [TeX:] $$|m|$$ tends to infinity, the speedup tends to n.
6.2 Experimental Result
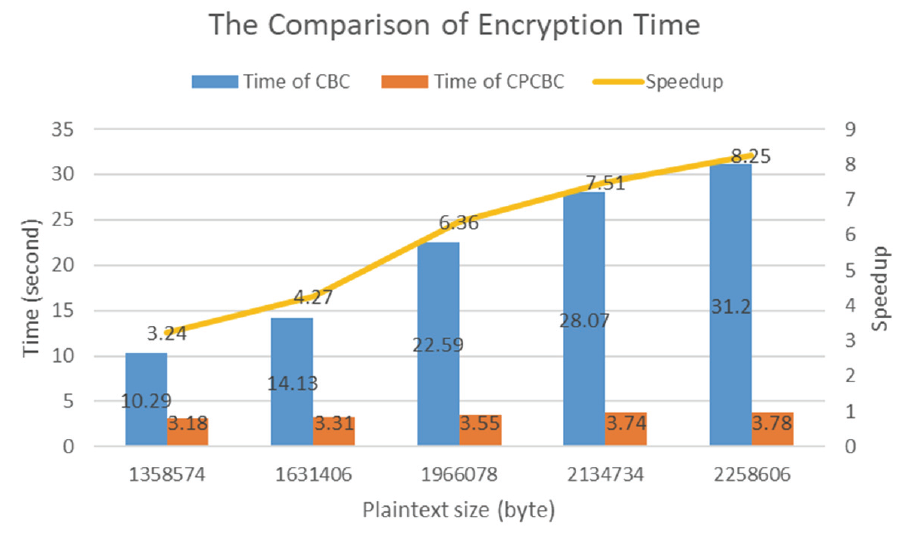
To validate the above analysis, 128-bit AES encryption is implemented in CBC mode and CPCBC mode, respectively, through the program, and the encryption time is measured. The program running environment of this paper is as follows: Intel Core i5-10210U CPU @1.60 GHz 2.11 GHz, 4 cores and 8 threads, 16 GB memory, and Python 3.9.8. The Crypto library is used for the implementation of AES, and the multiprocessor effect is simulated using multiple processes. To achieve a better simulation effect, parallelism is selected as n=8. Table 3 and Fig. 2 show the time consumption and comparison of encryption obtained by running the program.
From Fig. 2, it is evident that as the plaintext size increases, the time consumption of CBC mode shows a significant increase, whereas the time consumption of CPCBC mode remains stable. Additionally, the speedup ratio is gradually approaching a parallelism of 8. Thus, the CPCBC mode exhibits a nearly linear acceleration ratio.
Table 3.
| Plaintext size (byte) | Time (s) | Time (s) | Speedup |
|---|---|---|---|
| CBC | CPCBC | ||
| 1358574 | 10.29 | 3.18 | 3.24 |
| 1631406 | 14.13 | 3.31 | 4.27 |
| 1966078 | 22.59 | 3.55 | 6.36 |
| 2134734 | 28.07 | 3.74 | 7.51 |
| 2258606 | 31.20 | 3.78 | 8.25 |
During decryption in CPCBC mode, there is no dependency between ciphertext blocks. This is because the receiver has all the blocks and the initialization vector IV. Therefore, CPCBC mode maintains the same decryption efficiency as conventional CBC mode. Table 4 provides a comparative analysis of the CPCBC mode and some common modes of operation.
Table 4.
| Modes of operation | CBC | CPCBC | ECB | CFB |
|---|---|---|---|---|
| Speedup (Based on CBC mode) | 1 | n | s | 1 |
| Parallelism of encryption | ✓ | ✓ | ||
| Parallelism of decryption | ✓ | ✓ | ✓ | ✓ |
| Security | ✓ | ✓ |
Therefore, this mode of operation has almost a linear acceleration ratio for encrypting large amounts of data. Compared with the conventional CBC mode, the encryption speed is much faster.
7. Conclusions
This paper presents a controllable parallel CBC mode, CPCBC. This mode of operation achieves an approximate linear acceleration ratio, allowing for flexible control of parallelism n while preserving the security features of the conventional CBC mode. It is proven secure under the LOR-CPA model. For BFA and POA, this scheme is more resistant without disclosing the degree of parallelism n and has a certain improvement in security compared with conventional CBC mode.
In future studies, we will explore the potential of combining the proposed CPCBC mode with homomorphic encryption to enhance the speed of homomorphic encryption. This will address the security concerns associated with delegating private data and operations to third parties.
Biography
Biography
Biography
Biography
References
- 1 K. Gafurov and T. M. Chung, "Comprehensive survey on internet of things, architecture, security aspects, applications, related technologies, economic perspective, and future directions," Journal of Information Processing Systems, vol. 15, no. 4, pp. 797-819, 2019. https://doi.org/10.3745/JIPS.03.0125doi:[[[10.3745/JIPS.03.0125]]]
- 2 M. Ke, Z. Gao, Y . Wu, X. Gao, and K. K. Wong, "Massive access in cell-free massive MIMO-based Internet of Things: cloud computing and edge computing paradigms," IEEE Journal on Selected Areas in Communications, vol. 39, no. 3, pp. 756-772, 2021. https://doi.org/10.1109/JSAC.2020.3018807doi:[[[10.1109/JSAC.2020.3018807]]]
- 3 M. Liskov, R. L. Rivest, and D. Wagner, "Tweakable block ciphers," Journal of cryptology, vol. 24, pp. 588613, 2011. https://doi.org/10.1007/s00145-010-9073-ydoi:[[[10.1007/s00145-010-9073-y]]]
- 4 Y . Zhou, J. Guo, and F. Li, "Certificateless public key encryption with cryptographic reverse firewalls," Journal of Systems Architecture, vol. 109, article no. 101754, 2020. https://doi.org/10.1016/j.sysarc.2020.101754doi:[[[10.1016/j.sysarc.2020.101754]]]
- 5 National Bureau of Standards, "DES Modes of Operation (FIPS 81)," 1980 (Online). Available: https://doi.org/10.6028/NBS.FIPS.81.doi:[[[10.6028/NBS.FIPS.81]]]
- 6 P . Rogaway, M. Bellare, and J. Black, "OCB: a block-cipher mode of operation for efficient authenticated encryption," ACM Transactions on Information and System Security , vol. 6, no. 3, pp. 365-403, 2003. https://doi.org/10.1145/937527.937529doi:[[[10.1145/937527.937529]]]
- 7 C. S. Jutla, "Encryption modes with almost free message integrity," Journal of Cryptology, vol. 21, pp. 547578, 2008. https://doi.org/10.1007/s00145-008-9024-zdoi:[[[10.1007/s00145-008-9024-z]]]
- 8 M. Bellare, P . Rogaway, and D. Wagner, "The EAX mode of operation," in Fast Software Encryption. Heidelberg, Germany: Springer, 2004, pp. 389-407. https://doi.org/10.1007/978-3-540-25937-4_25doi:[[[10.1007/978-3-540-25937-4_25]]]
- 9 A. Y . Grama, A. Gupta, and V . Kumar, "Isoefficiency: measuring the scalability of parallel algorithms and architectures," IEEE Parallel & Distributed Technology: Systems & Applications , vol. 1, no. 3, pp. 12-21, 1993. https://doi.org/10.1109/88.242438doi:[[[10.1109/88.242438]]]
- 10 A. M. El-Semary and M. M. A. Azim, "Counter chain: a new block cipher mode of operation," Journal of Information Processing Systems, vol. 11, no. 2, pp. 266-279, 2015. http://dx.doi.org/10.3745/JIPS.03.0031doi:[[[10.3745/JIPS.03.0031]]]
- 11 A. Sahi, D. Lai, and Y . Li, "An efficient hash based parallel block cipher mode of operation," in Proceedings of 2018 3rd International Conference on Computer and Communication Systems (ICCCS), Nagoya, Japan, 2018, pp. 33-40. https://doi.org/10.1109/CCOMS.2018.8463342doi:[[[10.1109/CCOMS.2018.8463342]]]
- 12 B. Kaliski, "RFC2315: PKCS# 7: Cryptographic Message Syntax version 1.5," 1998 (Online). Available: https://dl.acm.org/doi/pdf/10.17487/RFC2315.custom:[[[https://dl.acm.org/doi/pdf/10.17487/RFC2315]]]
- 13 M. Bellare, A. Desai, E. Jokipii, and P . Rogaway, "A concrete security treatment of symmetric encryption," in Proceedings 38th Annual Symposium on Foundations of Computer Science, Miami Beach, FL, USA, 1997, pp. 394-403. https://doi.org/10.1109/SFCS.1997.646128doi:[[[10.1109/SFCS.1997.646128]]]
- 14 S. V audenay, "Security flaws induced by CBC padding: applications to SSL, IPSEC, WTLS...," in Advances in Cryptology - EUROCRYPT 2002. Heidelberg, Germany: Springer, 2002, pp. 534-545. https://doi.org/10.1007/3-540-46035-7_35doi:[[[10.1007/3-540-46035-7_35]]]