Xiuye Yin and Liyong Chen
Task Scheduling and Resource Management Strategy for Edge Cloud Computing Using Improved Genetic Algorithm
Abstract: To address the problems of large system overhead and low timeliness when dealing with task scheduling in mobile edge cloud computing, a task scheduling and resource management strategy for edge cloud computing based on an improved genetic algorithm was proposed. First, a user task scheduling system model based on edge cloud computing was constructed using the Shannon theorem, including calculation, communication, and network models. In addition, a multi-objective optimization model, including delay and energy consumption, was constructed to minimize the sum of two weights. Finally, the selection, crossover, and mutation operations of the genetic algorithm were improved using the best reservation selection algorithm and normal distribution crossover operator. Furthermore, an improved legacy algorithm was selected to deal with the multi-objective problem and acquire the optimal solution, that is, the best computing task scheduling scheme. The experimental analysis of the proposed strategy based on the MATLAB simulation platform shows that its energy loss does not exceed 50 J, and the time delay is 23.2 ms, which are better than those of other comparison strategies.
Keywords: Edge Cloud Computing , Energy Consumption , Improved Genetic Algorithm , Normal Distribution Crossover Operator , Resource Management , Task Scheduling , Time Delay
1. Introduction
As one of the key cores of the information industry, cloud computing has developed rapidly with strong support from the state and society. Mobile cloud computing (MCC) realizes the decentralization of cloud computing services, allowing users to access cloud resources anytime and anywhere without being constrained by space and computing equipment [1]. Owing to the limitations of portability and mobility, mobile devices generally have restricted computing and storage performances, which cannot meet the needs of users for computing-intensive and delay-sensitive applications. Therefore, computing offloading technologies have emerged [2,3]. This technology saves local resources by sending local computing tasks to locations with abundant computing resources.
However, the wireless communication environment between mobile devices and edge cloud has an important impact on task offloading performance and directly affects the decision of mobile user equipment to perform task offloading [4]. Currently, research on mobile edge computing (MEC) focuses on single-objective optimization to reduce system delay or energy consumption [5]. Examples of this include the elastic load-balancing scheme proposed for the problem of node load imbalance resulting from abundant parallel computing in a cloud environment, the distributed algorithm offloading strategy using game theory, and the wireless network offloading strategy using binary computing methods [6]. Li and Jiang [7] suggested a distributed task-unloading strategy for low-load base station groups that used the potential game model as the solution. This effectively alleviated the energy consumption of distributed task offloading; however, the communication delay was relatively high. Regarding the role of fog computing in reducing latency and saving energy consumption, Luo et al. [8] proposed a resource cooperation incentive mechanism to execute different equipment tasks combined with alliance game theory. This mechanism effectively realized the scheduling and distribution of computing tasks. Although it reduced the energy consumption of mobile devices, it increased computing and communication energy consumption, thereby requiring further optimization. In [9], a decentralized algorithm was developed based on a computational equilibrium strategy. This algorithm was used to calculate task offloading decisions between local devices and edge clouds and achieve efficient task offload classification; however, it had a high degree of dependence on average system parameters. Josilo and Dan [10] investigated the offloading of computing tasks and application program division and conducted an in-depth investigation of various offloading strategies to save the enforcement time of computing tasks for mobile devices and extend their endurance. The abovementioned offloading strategy is mainly optimized for a single goal in the system, and simultaneously meeting the requirements of low energy loss and low latency for multiuser and multitask applications is difficult [11].
In line with the rise in computing power and communication technology, intelligent algorithms have been widely used in the field of multi-objective optimization. For example, Xu et al. [12] suggested a computing task offloading method based on cloud edge computing of the Internet of Things (IoT). A non-dominated sorting genetic algorithm was used to address the problem of multi-objective optimization of the cloud edge computing task offloaded by the algorithm; however, the overall efficiency of the algorithm requires improvement. Zhou et al. [13] proposed a computational unloading method based on contract theory and computational intelligence. The incentive mechanism and contract theory were used to encourage the server to share its remaining computing resources, and the online learning ability of the multi-arm slot machine was used to propose a distributed task offloading algorithm. It effectively reduced the task offloading delay; however, an improvement in the offloading efficiency of computing tasks is still required for computing-intensive applications. With reference to the problem of limited computing power in connected car equipment, Liu et al. [14] proposed two computing task offloading strategies: partial and binary offloading. Binary offloading reduces the latency of processing computationally intensive tasks, whereas partial offloading improves the real-time performance of processing divisible complex tasks and reduces energy consumption. However, the advantages of the two methods have not been deeply integrated, and timeliness and energy consumption optimization cannot be balanced.
Based on the above analysis, an edge cloud computing task scheduling and resource management strategy based on improved genetic algorithms was proposed to solve the problems of timeliness and energy consumption optimization in the process of IoT edge cloud computing task scheduling and resource management. The contributions of this study are as follows:
(1) To improve resource management efficiency, the suggested strategy uses edge cloud computing to build a task scheduling model. Through optimized decision-making, some tasks are offloaded to edge cloud servers for calculation, which ensures time-consuming calculations and reduces system energy consumption.
(2) Considering the premature convergence of genetic algorithms leading to the high overhead of offloading algorithms, the proposed strategy improves the mutation and crossover processes of the genetic algorithm and combines the normal distribution crossover (NDX) operator to expand the feasible solution range. This can enhance the search efficiency and accuracy of the algorithm, avoid premature convergence, and reduce system overhead.
2. System Model and Optimization Goal
2.1 System Model
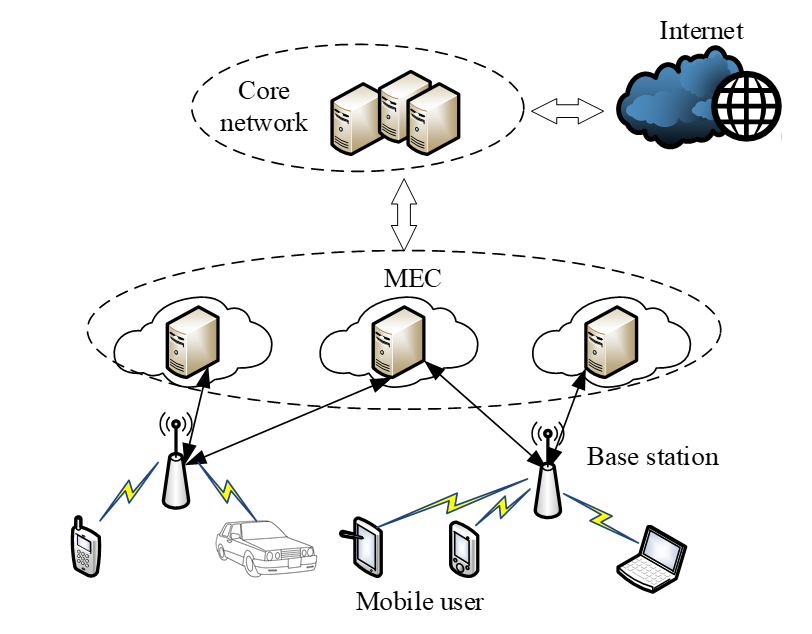
According to previous research results on MCC and mobile communication networks, the design of mobile user scheduling tasks is in a quasistatic scenario. Fig. 1 shows the system model. [TeX:] $$k=\{1,2, \cdots, K\}$$ mobile device users are randomly distributed around the base station, and user-computing tasks are scheduled to the MEC server through the base station for computing.
In this system model, all users with task scheduling requirements keep their scheduling and offloading strategies unchanged during the process of computing offloading to the MEC server, which typically lasts a few hundred milliseconds. This does not affect the user's later policy changes and maintains the stability of the system.
2.2 Communication Model
In general, the mobile operator determines the communication rate between mobile device users and base stations, that is, the state of the data transmission channel, uplink transmission rate, and downlink transmission rate. The improvement in 3G, 4G, and 5G network speeds also improves and expands communication operators’ technology and resources. The system design has [TeX:] $$q=\{1,2, \cdots, Q\}$$ wireless transmission channels between the user and the base station, and [TeX:] $$a_k$$ is the computing offloading strategy of user k. [TeX:] $$a_k=0$$ indicates that the user places computing tasks on the local mobile terminal to run, whereas [TeX:] $$a_k \gt 0$$ indicates that the user offloads computing tasks to the MEC terminals to run through a wireless channel, which is expressed as follows:
Then, [TeX:] $$a_{1-K}=\left(a_1, a_2, \cdots, a_K\right)$$ is the task scheduling strategy for all users, and the definition of the Shannon spectrum formula is used to obtain the data uplink transmission rate when mobile users choose to schedule tasks in the cloud. The channel capacity [TeX:] $$C_k$$ is evaluated as follows:
where W represents the channel bandwidth; [TeX:] $$S_k=\rho_k \kappa_k, \rho_k \text { and } \kappa_k$$ are the transmission power density and channel gain of communication between user k and the base station, respectively; and [TeX:] $$N_i=\sigma+\sum_{i \in\{K\} ; a_i=a_n}^K \rho_i \kappa_i \text { and } \sigma$$ are background white noise interference. If multiple users share the same channel to transmit data in a wireless cellular network, mutual interference will occur, which will reduce system performance and increase user load. Therefore, mutual interference is not considered for the time being.
2.3 Calculation Model and Optimization Goal
Assuming that the tasks in the scenario are independent of each other, each task can be executed locally, or all or part of the tasks can be uploaded to the cloud for enforcement. Let matrix [TeX:] $$\Omega_n=\left(D_n, \varphi_n, \alpha_n, \tau_n\right)$$ denote task n, where [TeX:] $$D_n$$ denotes the amount of data uploaded by task n including the parameters and code blocks required for the calculation. [TeX:] $$0\lt \varphi_n\lt 1$$ represents the ratio of task n intensive task data volume to the overall data volume. The larger [TeX:] $$\varphi_n$$ is, the more CPU resources are required for computing tasks and the greater the time complexity. [TeX:] $$0 \leq \alpha_n \leq 1$$ represents the offload rate of task n, [TeX:] $$\alpha_n=0$$ represents that task n is executed locally, and [TeX:] $$\alpha_n=1$$ represents that task n is implemented remotely at the edge, cloud, etc. [TeX:] $$\tau_n$$ represents the maximum tolerance of task n to delay. If the threshold is exceeded, user experience cannot be guaranteed.
The delay in executing tasks locally is related to factors such as terminal computing power and data size. The delay of the local computer performing task n is
where [TeX:] $$f_n$$ is the CPU frequency of local computer to execute task n.
The computation expression for computing the energy consumption of local execution task n is
where [TeX:] $$Z_n$$ indicates the energy consumed in the unit CPU cycle of the computer to execute task n, and [TeX:] $$Z_n=10^{-27} f_n^2.$$
When task n is implemented locally, the delay and energy consumption costs are
where [TeX:] $$0 \lt \omega_n \lt 1$$ represents the delay weighting factor of task n. The closer [TeX:] $$\omega_n$$ is to 1, the more sensitive the task is to delays. [TeX:] $$1-\omega_n$$ is the energy consumption weighting factor for task n. The closer [TeX:] $$1-\omega_n$$ is to 1, the more sensitive the task is to energy consumption. It is assumed that the delay weighting factor and energy consumption weighting factor are equal; that is, both are 0.5.
If all tasks are executed locally, the delay and energy consumption costs are
In addition, users can upload a part of the tasks or all tasks to the cloud or edge for execution. The cloud processing task is divided into the following three steps. First, users upload the task code and parameters required for the calculation to the edge or cloud server through a wireless access network. Second, the server distributes the calculation resources to the task and completes the calculation after receiving a task request. Finally, users download the result of the calculation using a downlink to complete task processing after completing the calculation.
Transmission delays occur when tasks are uploaded to the cloud. The calculation expression of upload task n transmission delay is
where [TeX:] $$v_n$$ represents the rate at which users upload task n.
Let [TeX:] $$\kappa_{k m}$$ denote the user k’s channel gain under the coverage of [TeX:] $$m(m=1,2, \cdots, M)$$ base station. [TeX:] $$P_m, P_k, \text { and } \delta^2$$ represent the transmission power of base station m, the uplink transmission power of user terminal k, and Gaussian white noise, respectively. The signal-to-noise ratio of user terminal k can be expressed as:
(8)
[TeX:] $$r_k=\frac{\left|\kappa_{k m}\right|^2 P_k}{\sum_m\left|\kappa_{k m}\right|^2 P_m+\delta^2}.$$Assume that W is the wireless channel bandwidth, and each cell and user terminal uses the same spectrum resources. Theoretically, the spectrum reuse factor is 1, and the maximum upload speed that user k can accomplish when uploading tasks is
User-upload tasks expend the energy of the terminal equipment, and the amount of energy consumed is related to the transmission time. Expressing the power of user W upload task as [TeX:] $$P_k,$$ the energy consumption of the user's upload task is
After the edge server receives the task, the task process causes calculation delays. Assume that the maximum computing power of the edge server is [TeX:] $$G_{\max },$$ and the computing resource allocated by the edge server for task n is [TeX:] $$G_n\left(G_n\lt G_{\max }())\right.$$. Multiuser and multitask requests for the computing resources of the edge server may simultaneously exceed the maximum computing ability of the edge server.
After the server receives the task request, the time delay for allocating the computing resources to the task and performing the calculation is
When a task is processed, the local terminal becomes idle. When the mobile edge server processes task n, that is, the standby energy consumption when the local terminal is in an idle state, the calculation expression is
where [TeX:] $$P_{\text {wait}, n}$$ represents the power consumed when the mobile edge server processes task n when the local terminal is idle.
After the edge/cloud server completes the calculation-intensive task, the mobile terminals download the calculation results using a downlink. Compared to the amount of data uploaded by users, the user only needs to download a smaller amount of calculation result data. The downlink has a fast download speed, and the overhead generated by the download is small, which can be ignored.
In summary, the overall cost of task n in the execution of edge computing services and cloud computing services is
(13)
[TeX:] $$F_{s e, n}=\omega_n\left(T_{t r, n}+T_{e x, n}\right)+\left(1-\omega_n\right)\left(E_{t r, n}+E_{i d, n}\right).$$Considering the local cost and edge/cloud cost comprehensively, the calculation expression of the overall system cost is
(14)
[TeX:] $$F_{\Sigma, n}=\omega_n\left(T_{t r, n}+T_{e x, n}+T_{l, n}\right)+\left(1-\omega_n\right)\left(E_{t r, n}+E_{i d, n}+E_{l, n}\right).$$Suppose the completion time limit of task is , and the optimization goal is to minimize the overall system overhead. Under the requirements of maximum system delay and maximum system ability, the proposed optimization objective function and constraint conditions can be expressed as
(15)
[TeX:] $$\begin{gathered} \min F_{\Sigma}=\sum_{n=1}^N F_{\Sigma, n}, \\ C 1: \alpha_n \in[0,1], \omega_n \in[0,1], \\ C 2: \frac{\left(1-\alpha_n\right) \varphi_n D_n}{f} \leq \tau, \\ C 3: \frac{\alpha_n D_n}{v_n}+\frac{\alpha_n \varphi_n D_n}{F_n} \leq \tau, \\ C 4: 0 \leq G_n \leq G_{\max }, \\ C 5: \sum_{n=1}^N G_n \leq G_{\max }. \end{gathered}$$3. Proposed Solution
The task calculation and distribution problem were converted into a nonlinear 0–1 programming problem, and a modified genetic algorithm was used to handle it. A feasible solution in the algorithm was determined by a chromosome, which corresponds to the corresponding task allocation strategy; that is, the optimal solution of the improved genetic algorithm is the optimal allocation strategy of the model.
3.1 Initialization Process
First, five aspects must be determined: maximum number of iterations, model parameters, crossover and mutation probabilities, chromosome length, and parameter set size, which represents the population size.
Maximum number of iterations: The number of iterations depends on the convergence of the algorithm, and the range of the number of iterations is generally [200, 500].
Migration model parameters: The parameters relevant to the previous article are separated into two types. One is the server resource information that must be obtained, and the other is calculated through historical data analysis or using the value set by the developer according to the actual situation. Regarding the data that must be obtained and stored in the database, one can directly connect to the database and fetch the latest data from the database into the formula in the algorithm.
Crossover and mutation probabilities: The value range of the crossover probability is generally between [0.1, 0.99]. When the chromosome changes, it affects the convergence accuracy and speed of the algorithm to a certain extent. Therefore, the mutation probability is relatively small, which is generally between [0.0001, 0.1].
Chromosome length: This refers to the number of mobile user tasks.
Parameter set size: This parameter is generally determined based on the number of tasks. For example, when the number of tasks is N, the size of the parameter set, that is, the size of the population, is [TeX:] $$2^{N / 2} \text {. }$$
3.2 Coding Process
When solving a system model, N task scheduling strategies are the values of variable [TeX:] $$\phi_n(n \in \{1, \cdots, N\})$$. Assuming that the number of tasks is N, the solution space of the algorithm is [TeX:] $$\left[0,2^N\right]$$, and the population size is [TeX:] $$2^{N / 2} .$$ It must convert [TeX:] $$2^{N / 2}$$ real numbers into binary form. For example, when N is 12, [TeX:] $$\left[0,2^{12}\right]$$ real numbers are randomly selected from the solution space [TeX:] $$2^{12 / 2}$$ as the initial population. At this time, the population size is [TeX:] $$2^{12 / 2}=64$$, and the 64 numbers must be coded. For example, if the real number 22 is randomly selected, the coding format of 12 gene positions represented by the real number is [0 0 0 0 1 0 1 0 1 1 0 1]. In the sequence format, “1” means that it is offloaded to the edge cloud server for calculation, and “0” means that the calculation is performed on the local server.
3.3 Fitness Function Construction
The traditional genetic algorithm selects individuals with higher fitness values to inherit the next generation. Thus, the reciprocal of the total user overhead was selected as the fitness function for evaluating the advantages and disadvantages of the chromosomes. The expression is as follows:
(16)
[TeX:] $$\text { fitness }=\frac{1}{\omega_n\left(T_{t r, n}+T_{e x, n}+T_{l, n}\right)+\left(1-\omega_n\right)\left(E_{t r, n}+E_{i d, n}+E_{l, n}\right)}.$$3.4 Select Operation
The concept of this strategy is to copy the best individuals (elite individuals) that have occurred in the evolution of a group directly to the next generation without pairing crossover, mutation, or other operations. Eiben used a Markov chain to prove that adding an elite retention strategy to genetic algorithms has global convergence. First, the fitness function was selected as the selection probability to build the roulette selection operator.
In the selection operation, each chromosome was first substituted into the selection probability as the offloading strategy, and the probability of selection [TeX:] $$\left[P_1, P_2, \cdots, P_n\right]$$ corresponding to each chromosome was then obtained. Moreover, the probability was accumulated to calculate [TeX:] $$\left[P_1, P_1+P_2, \cdots, P_1+P_2+\cdots+P_n\right],$$ and [TeX:] $$2^{N / 2}$$ random numbers were generated within the range of [TeX:] $$\left[0, P_1+P_2+\cdots+P_n\right] .$$ The random numbers in which intervals in the [TeX:] $$\left[P_1, P_1+P_2, \cdots, P_1+P_2+\cdots+P_n\right]$$ range were compared, and the chromosomes corresponding to the probability value of selection in this interval were selected to get a new population. Finally, elite individuals were retained without mutation and crossover operations. It was copied to the next generation in the next iteration as a new population individual.
3.5 Crossover Operation
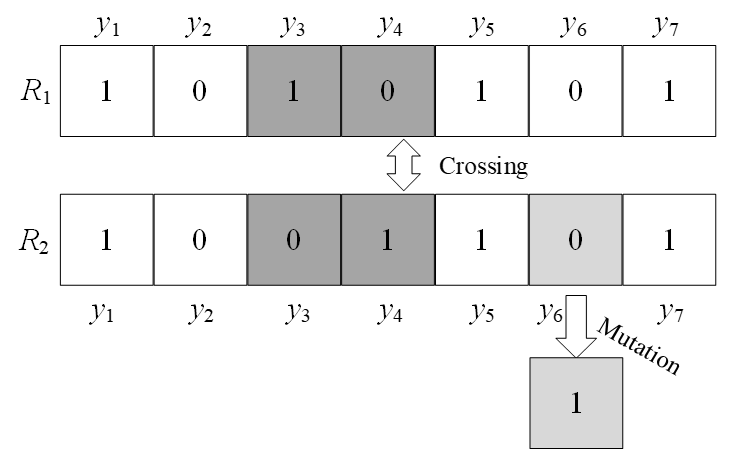
After retaining some of the gene fragments for the parent, the crossover operation of the improved genetic algorithm generated new offspring and extended the range of feasible solutions. Examples of crossover and mutation are shown in Fig. 2.
Suppose that the chromosomes of the parent population are [TeX:] $$R_1 \text { and } R_2$$, which use the NDX operator to generate offspring as [TeX:] $$b_1 \text { and } b_2$$. The crossover operation was separated into the following steps:
Step 1: Randomly generate number [TeX:] $$h \in 0,1 .$$
Step 2: Cross.
If [TeX:] $$h \leq 0.5$$, the crossover operation modes of i gene [TeX:] $$b_{1, i}$$ of offspring 1 and i gene [TeX:] $$b_{2, i}$$ of the generated offspring 2 are
(17)
[TeX:] $$\begin{aligned} b_{1, i}=\frac{y_{1, i}+y_{2, i}}{2}+\frac{1.481\left(y_{1, i}-y_{2, i}\right)|N(0,1)|}{2}, \\ b_{2, i}=\frac{y_{1, i}+y_{2, i}}{2}-\frac{1.481\left(y_{1, i}-y_{2, i}\right)|N(0,1)|}{2}, \end{aligned}$$where [TeX:] $$y_{1, i} \text { and } y_{2, i}$$ indicate the i genes of chromosomes [TeX:] $$R_1 \text { and } R_2 \text {, }$$ respectively; [TeX:] $$\frac{1.481\left(y_{1, i}-y_{2, i}\right)}{2}$$ is the size of the search step, and the ratio coefficient of the search step size to [TeX:] $$\frac{\left(y_{1, i}-y_{2, i}\right)}{2}$$ is 1.481.
If [TeX:] $$h \leq 0.5 \text {, }$$ the crossover operation models are:
4. Experiment and Analysis
4.1 Experimental Setup
The proposed method was verified using the MATLAB 2016 simulation platform. The simulation parameters are listed in Table 1. It is assumed that only Gaussian white noise interference exists. Suppose that the communication cell deploys an intelligent base station with sufficient computing power. Various potential users are randomly distributed in the cell.
Table 1.
| Parameter | Value |
|---|---|
| Computing capability of mobile devices (cycles/s) | [TeX:] $$6 \times 10^2$$ |
| Standby power of mobile devices (W) | [TeX:] $$1.0 \times 10^{-3}$$ |
| Transmitting power of mobile devices (W) | [TeX:] $$0.5 \times 10^{-1}$$ |
| Computing power of edge devices (cycles/s) | [TeX:] $$3 \times 10^3$$ |
| Edge offloading delay (ms) | 1.2 |
| Cloud computing capability (cycles/s) | [TeX:] $$4 \times 10^3$$ |
| Cloud offloading delay (ms) | 20 |
| Channel bandwidth (kB/s) | [TeX:] $$1.0 \times 10^2$$ |
| Calculated power of mobile devices (W) | [TeX:] $$6 \times 10^{-1}$$ |
| Gaussian white noise power (W) | [TeX:] $$1.0 \times 10^{-9}$$ |
| Number of users | [10,50], uniform distribution |
4.2 Performance Comparison
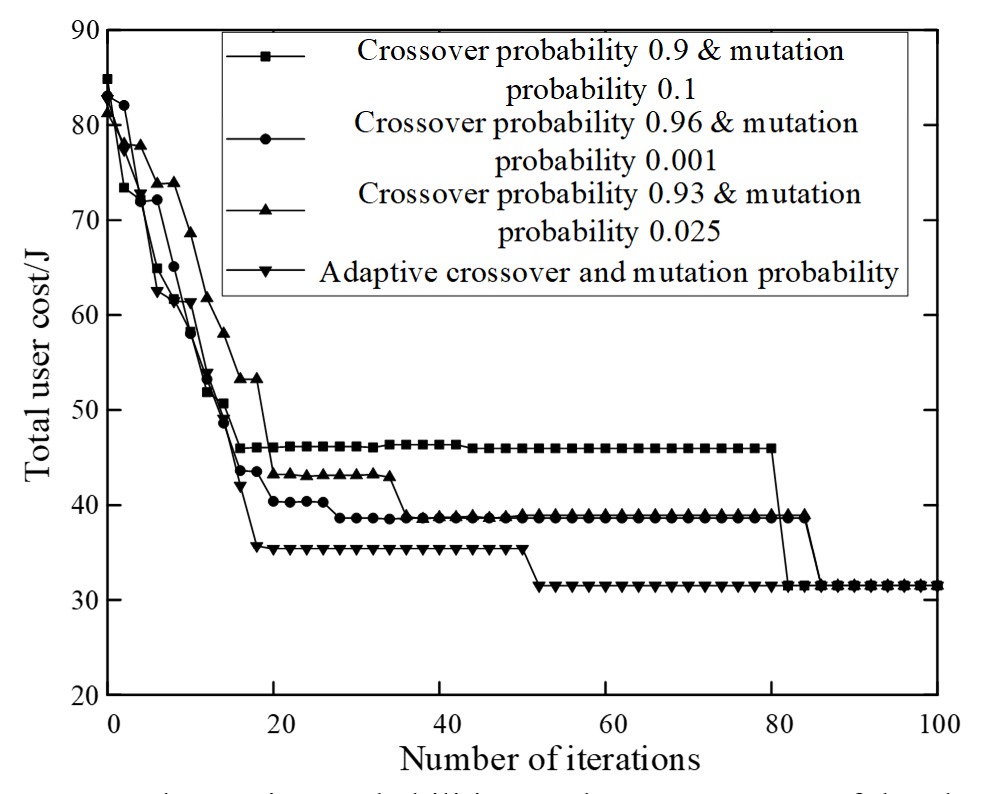
Improving the crossover and mutation probabilities of a genetic algorithm has a certain impact on the convergence of the algorithm. The total user overhead results under different crossover and mutation probabilities when the number of users is 30 are shown in Fig. 3.
As shown in Fig. 3, when a fixed crossover and mutation probability are given, the algorithm reaches a local optimal solution, and the search process is lengthened. The adaptive crossover and mutation probabilities can be dynamically adjusted using the fitness value to prevent entering the local optimal solution. Compared to fixed crossover probability and mutation probability settings, the proposed algorithm has obvious advantages and fast convergence speed. When the number of iterations is 50, the total user overhead tends to converge to 32 J approximately.
The result of the iteration is shown in Fig. 4.
As shown in Fig. 4, when the number of iterations increases, the total user overhead of the improved genetic algorithm is lower than that of the genetic algorithm by approximately 7 J. Because the improved genetic algorithm uses the NDX operator to update the crossover and mutation probabilities, it can avoid falling into the local optimum. Therefore, it gradually converges at 50 iterations and finally approaches approximately 32 J. However, the genetic algorithm easily reaches the local optimum. In addition, the convergence process fluctuates significantly; when the number of iterations is 100, the total user overhead is 39 J.
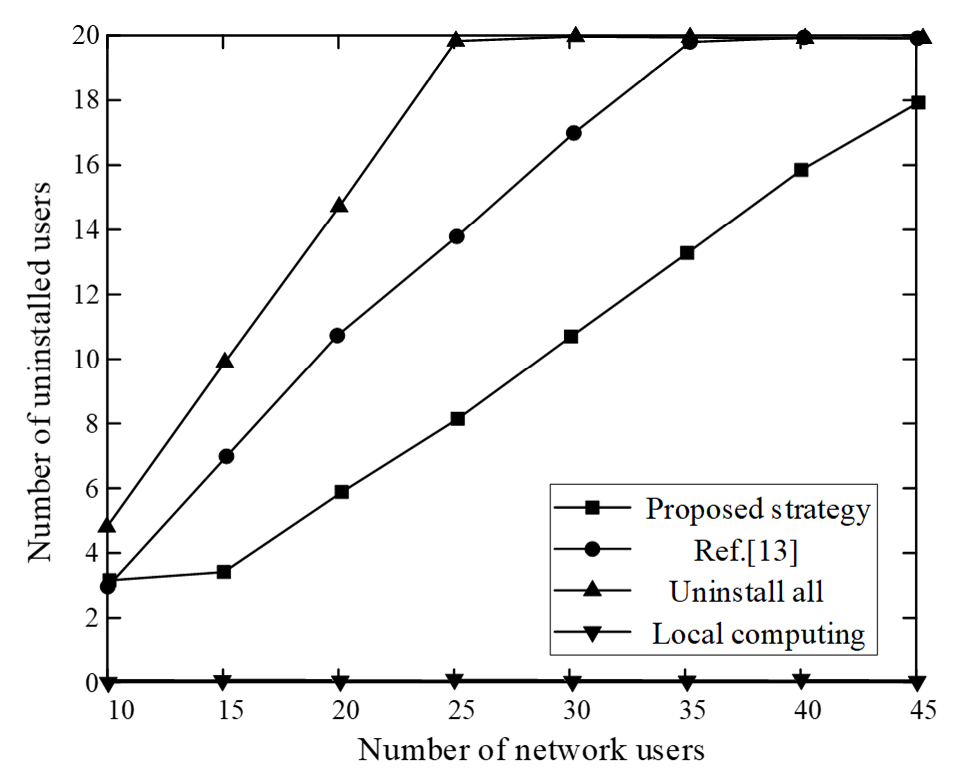
The relationship between the total number of network users and the number of offloading users is shown in Fig. 5.
Fig. 5 shows that as all computing tasks are processed locally, task scheduling does not occur. Therefore, the number of offloading users is always 0. When choosing to offload all tasks, until the number of users is greater than 30, the system bandwidth is exhausted, and the remaining users who have not been offloaded can only choose to process tasks locally. Zhou et al. [13] did not consider the limitations of system bandwidth. When the number of users is greater than 35, the system bandwidth is close to saturation, and users cannot choose to offload tasks. The suggested strategy can maximize the use of the system bandwidth and appropriately select the number of offloaded users compared with the other three strategies, thereby improving system utility. When the number of network users reaches 45, the number of offloading users is only 18. The system still has the capabilities of task offloading and resource management.
To demonstrate the performance of the proposed strategy, we compared the total system overhead obtained by the local calculation of all network users, all offloading users, the strategy in [13], and our proposed strategy in terms of different numbers of users. The results are shown in Fig. 6.
As shown in Fig. 6, channel congestion and inter-user interference increase so rapidly that the system overhead for users to select the all-offloading strategy is greater than the local computing overhead when there are more than 30 users in the system. Therefore, designing an edge cloud computing environment requires designing the hardware configuration of the base stations and MEC servers according to the number of edge users to meet the needs of mobile users. In addition, Zhou et al. [13] realized task offloading and resource sharing in two stages by combining contract theory and computational intelligence. The incentive mechanism and contract theory were used to encourage the server to share its remaining computing resources, and the multi-arm slot machine algorithm was used for online learning to complete distributed task offloading. Thus, the system energy consumption can be effectively reduced; however, the offloading process is complicated, which undoubtedly increases the calculation and communication energy consumption to a certain extent. The proposed strategy was based on edge cloud computing for task scheduling, and the best resource management plan was obtained by improving a genetic algorithm. The whole process is simple and efficient, resulting in low energy consumption. The total system overhead is less than 50 J when the number of users is 50.
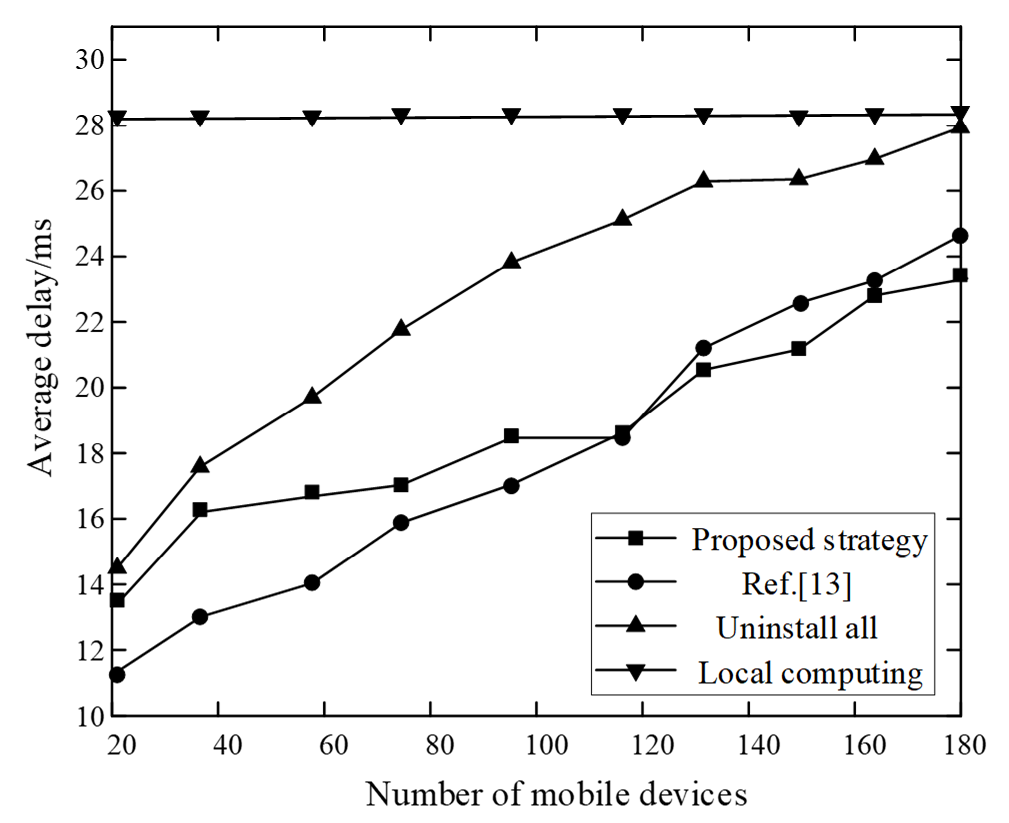
Similarly, considering different numbers of users, we compared the average delay of all users’ local computing, all offloading, the strategy in [13], and the mobile user’s task execution in the proposed strategy, as shown in Fig. 7.
Fig. 7 clearly shows that when the number of mobile devices increases, the average delay of the proposed strategy increases slowly, and the advantages become more evident. The average delay is approximately 23.2 ms when the number of devices is 180. This is because the proposed cloud-side collaboration model is used to construct the task scheduling model, and an improved genetic algorithm is selected to handle the problem; hence, the best resource management plan can be obtained. It can comprehensively consider local and cloud computing resources to accomplish both minimum energy consumption and minimum delay. The average delay of the local calculation strategy is constant at approximately 28.1 ms. Because all computing tasks were performed locally, there was no offloading delay. When the full offloading strategy is adopted, the more mobile devices there are, and the more exhausted the communication bandwidth is will tend to be exhausted; thus, the resulting offloading delay will continues to increase. When the number of devices reaches 180, the average delay is close to 28 ms. Zhou et al. [13] proposed a two-stage resource-sharing and task-offloading method, which used the incentive mechanism and contract theory were used to spur servers to share their remaining computing resources. Although it can achieve better task scheduling better, the complex contract theory and offloading process increase the system delay. Therefore, the average delay increases rapidly, exceeding 24 ms, as the number of devices increases.
5. Conclusion
In recent years, the number of mobile Internet users with mobile smart terminals has increased with the continuous popularization of cloud computing technology and the ongoing advancements of mobile network technology. Edge cloud computing has emerged to meet the business requirements of ultralow latency and power consumption, ultrahigh reliability, and density. Based on this, an edge cloud computing task scheduling and resource management strategy using an improved genetic algorithm was proposed. In addition, a user task scheduling system model was constructed based on edge cloud computing, and an improved legacy algorithm was selected to handle the multi-objective optimization function, including time delay and energy consumption. The optimal solution for the algorithm is the best resource management plan. A simulation experiment of the suggested strategy was implemented based on MATLAB, and the results of the experiment confirm the following conclusions:
(1) Optimizing the crossover and mutation operations of the genetic algorithm using the NDX operator can increase the convergence speed and optimization performance of the algorithm. Convergence was achieved when the number of iterations was 50, and the total system overhead was reduced by approximately 7 J compared with traditional genetic algorithms.
(2) The proposed strategy combined edge cloud computing and intelligent algorithms for task scheduling. The energy consumption during this period was less than 50 J, and the average delay was 23.2 ms. The experimental results indicate that the overall performance of the proposed strategy is better than that of the comparison strategy.
To reduce the difficulty in deriving a theoretical formula, some system model parameters were set to constant values in the simulation experiment. In future work, we will impose fewer restrictions on the model parameters, and more consideration will be given to the dynamic changes in the parameter weights in the model. Moreover, the addition of simulation experimental samples will enable the real-life applications of the proposed model algorithm.
Biography
Biography
Liyong Chen
https://orcid.org/0000-0002-8570-591XHe was born in 1982, male, Chinese, He received master's degree in School of Com-puter Science and Technology, Faculty of Electronic Information, Liaoning University of Science and Technology, China, in 2010. He has been teaching at Zhoukou Normal University since 2010. His research interests include artificial intelligence and data mining.
References
- 1 D. Madeo, S. Mazumdar, C. Mocenni, and R. Zingone, "Evolutionary game for task mapping in resource constrained heterogeneous environments," Future Generation Computer Systems, vol. 108, pp. 762-776, 2020. https://doi.org/10.1016/j.future.2020.03.026doi:[[[10.1016/j.future.2020.03.026]]]
- 2 E. H. Lee and S. Lee, "Task offloading algorithm for mobile edge computing," Journal of Korean Institute of Communications and Information Sciences, vol. 46, no. 2, pp. 310-313, 2021. https://doi.org/10.7840/kics. 2021.46.2.310doi:[[[10.7840/kics.2021.46.2.310]]]
- 3 A. R. Arunarani, D. Manjula, and V . Sugumaran, "Task scheduling techniques in cloud computing: a literature survey," Future Generation Computer Systems, vol. 91, pp. 407-415, 2019. https://doi.org/10.1016/j.future. 2018. 09.014doi:[[[10.1016/j.future.2018.09.014]]]
- 4 P. P. Hung, M. G. R. Alam, H. Nguyen, T. Quan, and E. N. Huh, "A dynamic scheduling method for collaborated cloud with thick clients," International Arab Journal of Information Technology, vol. 16, no. 4, pp. 633-643, 2019.custom:[[[https://khu.elsevierpure.com/en/publications/a-dynamic-scheduling-method-for-collaborated-cloud-with-thick-cli-2]]]
- 5 G. Lou and Z. Cai, "A cloud computing oriented neural network for resource demands and management scheduling," International Journal of Network Security, vol. 21, no. 3, pp. 477-482, 2019. https://doi.org/ 10.6633/IJNS.201905_21(3).14doi:[[[10.6633/IJNS.20_21(3).14]]]
- 6 X. Huang, C. Li, H. Chen, and D. An, "Task scheduling in cloud computing using particle swarm optimization with time varying inertia weight strategies," Cluster Computing, vol. 23, pp. 1137-1147, 2020. https://doi.org/ 10.1007/s10586-019-02983-5doi:[[[10.1007/s10586-019-02983-5]]]
- 7 Y . Li and C. Jiang, "Distributed task offloading strategy to low load base stations in mobile edge computing environment," Computer Communications, vol. 164, pp. 240-248, 2020. https://doi.org/10.1016/j.comcom. 2020.10.021doi:[[[10.1016/j.comcom.2020.10.021]]]
- 8 S. Luo, X. Chen, Z. Zhou, X. Chen, and W. Wu, "Incentive-aware micro computing cluster formation for cooperative fog computing," IEEE Transactions on Wireless Communications, vol. 19, no. 4, pp. 2643-2657, 2020. https://doi.org/10.1109/TWC.2020.2967371doi:[[[10.1109/TWC.2020.2967371]]]
- 9 S. Josilo and G. Dan, "Decentralized algorithm for randomized task allocation in fog computing systems," IEEE/ACM Transactions on Networking, vol. 27, no. 1, pp. 85-97, 2019. https://doi.org/10.1109/TNET.2018. 2880874doi:[[[10.1109/TNET.2018.2880874]]]
- 10 G. Sakarkar, N. Purohit, N. S. Gour, S. B. Meshram, "A review of computational task offloading approaches in mobile computing," International Journal of Scientific Research in Science, Engineering and Technology, vol. 6, no. 2, pp. 381-387, 2019. https://doi.org/10.32628/IJSRSETdoi:[[[10.32628/IJSRSET]]]
- 11 W. Li, S. Cao, K. Hu, J. Cao, and R. Buyya, "Blockchain-enhanced fair task scheduling for cloud-fog-edge coordination environments: model and algorithm," Security and Communication Networks, vol. 2021, article no. 5563312, 2021. https://doi.org/10.1155/2021/5563312doi:[[[10.1155/2021/5563312]]]
- 12 X. Xu, Q. Liu, Y . Luo, K. Peng, X. Zhang, S. Meng, and L. Qi, "A computation offloading method over big data for IoT-enabled cloud-edge computing," Future Generation Computer Systems, vol. 95, pp. 522-533, 2019. https://doi.org/10.1016/j.future.2018.12.055doi:[[[10.1016/j.future.2018.12.055]]]
- 13 Z. Zhou, H. Liao, B. Gu, S. Mumtaz, and J. Rodriguez, "Resource sharing and task offloading in IoT fog computing: a contract-learning approach," IEEE Transactions on Emerging Topics in Computational Intelligence, vol. 4, no. 3, pp. 227-240, 2020. https://doi.org/10.1109/TETCI.2019.2902869doi:[[[10.1109/TETCI.2019.2902869]]]
- 14 J. Liu, S. Wang, J. Wang, C. Liu, and Y . Yan, "A task oriented computation offloading algorithm for intelligent vehicle network with mobile edge computing," IEEE Access, vol. 7, pp. 180491-180502, 2019. https://doi. org/10.1109/ACCESS.2019.2958883custom:[[[-]]]